题目内容
 如图,已知BC是半径为1的半圆O的直径,A是半圆周上不同于B,C的点,又DC⊥面ABC,四边形ACDE为梯形,DE∥AC,且AC=2DE,DC=2,二面角B-DE-C的大小为θ,tanθ=
如图,已知BC是半径为1的半圆O的直径,A是半圆周上不同于B,C的点,又DC⊥面ABC,四边形ACDE为梯形,DE∥AC,且AC=2DE,DC=2,二面角B-DE-C的大小为θ,tanθ=| 3 | 4 |
(1)证明:面ABE⊥面ACDE;
(2)求四棱锥B-ACDE的体积.
分析:(1)由题意易得BA⊥DC,又AC∩DC=C,可判BA⊥面ACDE,再由面面垂直的判断定理可得结论;
(2)延长DE到F,使DF=AC,连接AF,BF,可证DF⊥AF,又可证BF⊥DF,可得∠AFB=θ,在RT△BAF中,由tanθ=
=
=
,可得BA=
,进而由勾股定理可得CA的长度,可得底面梯形的面积,而四棱锥B-ACDE的高为BA,代入体积公式可得答案.
(2)延长DE到F,使DF=AC,连接AF,BF,可证DF⊥AF,又可证BF⊥DF,可得∠AFB=θ,在RT△BAF中,由tanθ=
| BA |
| AF |
| BA |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
解答:解:(1)∵BC是直径,∴BC⊥CA,又DC⊥面ABC,所以BA⊥DC,
又AC∩DC=C,AC,DC?面ACDE,∴BA⊥面ACDE,
又BA?面ABE,所以面ABE⊥面ACDE;
(2)延长DE到F,使DF=AC,连接AF,BF,
∵DC⊥AC,∴四边形ACDF为矩形,∴DF⊥AF,
由(1)BA⊥DF,AF∩BA=A,∴DF⊥面BAF,∴BF⊥DF,
∴∠AFB为二面角B-DE-C的平面角,即∠AFB=θ,
在RT△BAF中,tanθ=
=
=
=
,∴BA=
,
∴CA=
=
=
,
由梯形的面积公式可得SACDE=
(
+
)×2=
,
由(1)知四棱锥B-ACDE的高为BA,
∴VB-ACDE=
×
×
=
又AC∩DC=C,AC,DC?面ACDE,∴BA⊥面ACDE,
又BA?面ABE,所以面ABE⊥面ACDE;
(2)延长DE到F,使DF=AC,连接AF,BF,
∵DC⊥AC,∴四边形ACDF为矩形,∴DF⊥AF,
由(1)BA⊥DF,AF∩BA=A,∴DF⊥面BAF,∴BF⊥DF,
∴∠AFB为二面角B-DE-C的平面角,即∠AFB=θ,
在RT△BAF中,tanθ=
| BA |
| AF |
| BA |
| CD |
| BA |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
∴CA=
| BC2-BA2 |
22-(
|
| ||
| 2 |
由梯形的面积公式可得SACDE=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
3
| ||
| 4 |
由(1)知四棱锥B-ACDE的高为BA,
∴VB-ACDE=
| 1 |
| 3 |
3
| ||
| 4 |
| 3 |
| 2 |
3
| ||
| 8 |
点评:本题考查平面与平面垂直的判定,涉及几何体体积的求解,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•蓝山县模拟)如图,已知BC是半径为1的半圆O的直径,A是半圆周上不同于B,C的点,F为
(2012•蓝山县模拟)如图,已知BC是半径为1的半圆O的直径,A是半圆周上不同于B,C的点,F为
 如图,已知BC是半径为1的半圆O的直径,A是半圆周上不同于B,C的点,F为
如图,已知BC是半径为1的半圆O的直径,A是半圆周上不同于B,C的点,F为 的中点.梯形ACDE中,DE∥AC,且AC=2DE,平面ACDE⊥平面ABC.求证:
的中点.梯形ACDE中,DE∥AC,且AC=2DE,平面ACDE⊥平面ABC.求证: 的中点.梯形ACDE中,DE∥AC,且AC=2DE,平面ACDE⊥平面ABC.求证:
的中点.梯形ACDE中,DE∥AC,且AC=2DE,平面ACDE⊥平面ABC.求证:
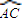 的中点.梯形ACDE中,DE∥AC,且AC=2DE,平面ACDE⊥平面ABC.求证:
的中点.梯形ACDE中,DE∥AC,且AC=2DE,平面ACDE⊥平面ABC.求证: