网址：http://m.1010jiajiao.com/timu_id_493572[举报]
一、填空题
(每题5分)
1)
2)
3)0 4)
5)
6) ②④ 7）
8）
9）
10）
11）
二、选择题 (每题5分)
12、A 13、B 14、B 15、D
三、解答题
16、
（1）因为
，所以∠BCA（或其补角）即为异面直线
与
所成角
-------(3分)
∠ABC=90°, AB=BC=1，所以
，
-------(2分)
即异面直线与所成角大小为
。
-------(1分)
（2）直三棱柱ABC-A1B
，所以
即为直线A
。 -------(2分)
中，AB=BC=1得到
，
中，得到
， -------(2分)
所以
-------(2分)
17、（10
=
-------(1分)
=
-------(1分)
=
-------(1分)
周期
； -------(1分)
，解得单调递增区间为
-------(2分)
（2）
，所以
，
，
所以
的值域为
，
-------(4分)
而
，所以
，即
-------(4分)
18、
，顾客得到的优惠率是
。 -------(5分)
(2)、设商品的标价为x元，则500≤x≤800 ------(2分)
消费金额： 400≤0.8x≤640
由题意可得：
（1）
≥
无解
------(3分)
或（2）
≥ 得：625≤x≤750 ------(3分)
因此，当顾客购买标价在
元内的商品时，可得到不小于的优惠率。------(1分)
19、（1）
与
轴的交点
为
， ------(1分)
；所以
，即
，-
----(1分)
因为
在上，所以
，即
----(2分)
（2）若
（
），
即若
（） ----(1分)
（A）当
时，
----(1分)
=
=
，而
，所以
----(1分)
（B）当
时，
----(1分)
= 
=
，
----(1分)
而
，所以
----(1分)
因此
（）
----(1分)
（3）假设存在
使得
成立。
（A）若为奇数，则
为偶数。所以
，
，而，所以
，方程无解，此时不存在。 ----(2分)
(B) 若为偶数，则为奇数。所以
，
，而，所以
，解得
----(2分)
由（A）（B）得存在
使得成立。
----(1分)
20、（1）（A）：点P与点F（2，0）的距离比它到直线＋4＝0的距离小2，所以点P与点F（2，0）的距离与它到直线＋2＝0的距离相等。 ----(1分)
由抛物线定义得：点
在以
为焦点直线＋2＝0为准线的抛物线上， ----(1分)
抛物线方程为
。 ----(2分)
解法（B）：设动点
，则
。当
时，
，化简得：
，显然
，而，此时曲线不存在。当时，
，化简得：。
（2）
，
，
，
----(1分)
，
，即
，
，
----(2分)
直线为
，所以
----(1分)
----(1分)
由（a）（b）得：直线恒过定点
。
----(1分)
设M是由满足下列两个条件的函数f(x)构成的集合：
①议程f(x)－x＝0有实根；②函数f(x)的导数
(x)满足0＜
(x)＜1．
(Ⅰ)若
，判断方程f(x)－x＝0的根的个数；
(Ⅱ)判断(Ⅰ)中的函数f(x)是否为集合M的元素；
(Ⅲ)对于M中的任意函数f(x)，设x1是方程f(x)－x＝0的实根，求证：对于f(x)定义域中任意的x2，x3，当|x2－x1|＜1，且|x3－x1|＜1时，有|f(x3)－f(x2)|＜2．
设M是由满足下列条件的函数f(x)构成的集合：“①方程f(x)－x＝0有实数根；②函数f(x)的导数
(x)满足0＜
(x)＜1．”
(Ⅰ)判断函数f(x)＝
＋
是否是集合M中的元素，并说明理由；
(Ⅱ)集合M中的元素f(x)具有下面的性质：若f(x)的定义域为D，则对于任意
[m，n]
D，都存在x0∈[m，n]，使得等式f(n)－f(m)＝(n－m)
(x0)成立．试用这一性质证明：方程f(x)－x＝0只有一个实数根；
(Ⅲ)对于M中的函数f(x)，设x1是方程f(x)－x＝0的实数根，求证：对于f(x)定义域中任意的x2，x3，当|x2－x1|＜1，且|x3－x1|＜1时，|f(x3)－f(x2)|＜2．
已知数列{an}满足：a1++ +…+＝n2+2n（其中常数λ＞0，n∈N*）.
（1）求数列{an}的通项公式；
（2）当λ＝4时，是否存在互不相同的正整数r，s，t，使得ar，as，at成等比数列？若存在，给出r，s，t满足的条件；若不存在，说明理由；
（3）设Sn为数列{an}的前n项和.若对任意n∈N*，都有(1-λ)Sn+λan≥2λn恒成立，求实数λ的取值范围.
查看习题详情和答案>>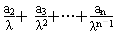
＝n2＋2n（其中常数λ＞0，n∈N*），