题目内容
已知数列{an}满足:a1+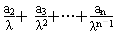 =n2+2n(其中常数λ>0,n∈N*),
=n2+2n(其中常数λ>0,n∈N*),
(1)求数列{an}的通项公式;
(2)当λ=4时,是否存在互不相同的正整数r,s,t,使得ar,as,at成等比数列?若存在,给出r,s,t满足的条件;若不存在,说明理由;
(3)设Sn为数列{an}的前n项和,若对任意n∈N*,都有(1-λ)Sn+λan≥2λn恒成立,求实数λ的取值范围。
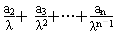 =n2+2n(其中常数λ>0,n∈N*),
=n2+2n(其中常数λ>0,n∈N*),(1)求数列{an}的通项公式;
(2)当λ=4时,是否存在互不相同的正整数r,s,t,使得ar,as,at成等比数列?若存在,给出r,s,t满足的条件;若不存在,说明理由;
(3)设Sn为数列{an}的前n项和,若对任意n∈N*,都有(1-λ)Sn+λan≥2λn恒成立,求实数λ的取值范围。
解:(1)当n=1时,a1=3;
当n≥2时,由a1+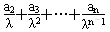 =n2+2n, ①
=n2+2n, ①
得 =(n-1)2+2(n-1), ②
=(n-1)2+2(n-1), ②
①-②得: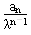 =2n+1,
=2n+1,
所以an=(2n+1)·λn-1,(n≥2),
因为a1=3,所以an=(2n+1)·λn-1(n∈N*)。
(2)当λ=4时,an=(2n+1)·4n-1,
若存在ar,as,at成等比数列,
则[(2r+1)4r-1] [(2t+1)·4t-1]=(2s+1)2·42s-2,
整理得(2r+1)(2t+1) 4r+t -2s=(2s+1)2,
由奇偶性知r+t -2s=0,
所以(2r+1)(2t+1)=(r+t+1)2,
即(r-t)2=0,
这与r≠t矛盾,
故不存在这样的正整数r,s,t,使得ar,as,at成等比数列。
(3)Sn=3+5λ+7λ2+…+(2n+1)λn-1,
当λ=1时,Sn=3+5+7+…+(2n+1)=n2+2n;
当λ≠1时,Sn=3+5λ+7λ2+…+(2n+1)λn-1,
λSn=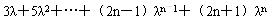 ,
,
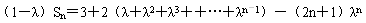
 ,
,
要对任意n∈N*,都有(1-λ)Sn+λan≥2λn恒成立,
①当λ=1时,左=(1-λ)Sn+λan=an=2n+1≥2,结论显然成立;
②当λ≠1时,
左=(1-λ)Sn+λan=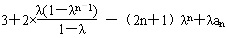
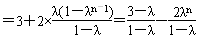 ,
,
因此,对任意n∈N*,都有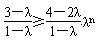 恒成立,
恒成立,
当0<λ<1时,只要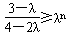 对任意n∈N*恒成立,
对任意n∈N*恒成立,
只要有 ,
,
因此,当0<λ<1时,结论成立;
当λ≥2时,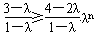 显然不可能对任意n∈N*恒成立;
显然不可能对任意n∈N*恒成立;
当1<λ<2时,只要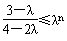 对任意n∈N*恒成立,
对任意n∈N*恒成立,
只要有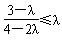 即可,解得1≤λ≤
即可,解得1≤λ≤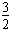 ;
;
因此当1<λ≤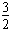 时,结论成立;
时,结论成立;
综上可得,实数λ的取值范围为(0, ]。
]。
当n≥2时,由a1+
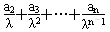 =n2+2n, ①
=n2+2n, ①得
 =(n-1)2+2(n-1), ②
=(n-1)2+2(n-1), ②①-②得:
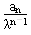 =2n+1,
=2n+1,所以an=(2n+1)·λn-1,(n≥2),
因为a1=3,所以an=(2n+1)·λn-1(n∈N*)。
(2)当λ=4时,an=(2n+1)·4n-1,
若存在ar,as,at成等比数列,
则[(2r+1)4r-1] [(2t+1)·4t-1]=(2s+1)2·42s-2,
整理得(2r+1)(2t+1) 4r+t -2s=(2s+1)2,
由奇偶性知r+t -2s=0,
所以(2r+1)(2t+1)=(r+t+1)2,
即(r-t)2=0,
这与r≠t矛盾,
故不存在这样的正整数r,s,t,使得ar,as,at成等比数列。
(3)Sn=3+5λ+7λ2+…+(2n+1)λn-1,
当λ=1时,Sn=3+5+7+…+(2n+1)=n2+2n;
当λ≠1时,Sn=3+5λ+7λ2+…+(2n+1)λn-1,
λSn=
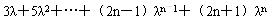 ,
,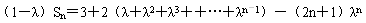
 ,
,要对任意n∈N*,都有(1-λ)Sn+λan≥2λn恒成立,
①当λ=1时,左=(1-λ)Sn+λan=an=2n+1≥2,结论显然成立;
②当λ≠1时,
左=(1-λ)Sn+λan=
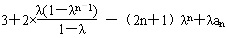
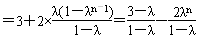 ,
,因此,对任意n∈N*,都有
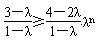 恒成立,
恒成立,当0<λ<1时,只要
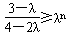 对任意n∈N*恒成立,
对任意n∈N*恒成立,只要有
 ,
,因此,当0<λ<1时,结论成立;
当λ≥2时,
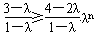 显然不可能对任意n∈N*恒成立;
显然不可能对任意n∈N*恒成立;当1<λ<2时,只要
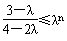 对任意n∈N*恒成立,
对任意n∈N*恒成立,只要有
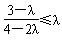 即可,解得1≤λ≤
即可,解得1≤λ≤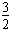 ;
;因此当1<λ≤
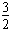 时,结论成立;
时,结论成立;综上可得,实数λ的取值范围为(0,
 ]。
]。
练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目