网址:http://m.1010jiajiao.com/timu_id_492727[举报]
一、选择题第一次月考数学试题.files/image220.gif)
1―5 BCAAB;6-10 BCACD ;11-12 DA
二、填空题
13、2 14、9 15、第一次月考数学试题.files/image222.gif) 16、②
16、②
三、解答题
17.解:
(Ⅰ)由第一次月考数学试题.files/image174.gif) ,得
,得第一次月考数学试题.files/image225.gif) ,
,
由第一次月考数学试题.files/image176.gif) ,得
,得第一次月考数学试题.files/image228.gif) .??????????????????????????????????????????????????????????????????????????????????????? 2分
.??????????????????????????????????????????????????????????????????????????????????????? 2分
所以第一次月考数学试题.files/image230.gif) .??????????????????????????????????????????? 5分
.??????????????????????????????????????????? 5分
(Ⅱ)由正弦定理得第一次月考数学试题.files/image232.gif) .?????????????????????????????????????????????????? 8分
.?????????????????????????????????????????????????? 8分
所以第一次月考数学试题.files/image036.gif) 的面积
的面积第一次月考数学试题.files/image235.gif)
第一次月考数学试题.files/image237.gif)
第一次月考数学试题.files/image239.gif) .????????????????????????? 10分
.????????????????????????? 10分
18.解:
(1)第一次月考数学试题.files/image241.gif)
第一次月考数学试题.files/image243.gif)
第一次月考数学试题.files/image245.gif) ,
, 第一次月考数学试题.files/image247.gif)
又椭圆的中心在原点,焦点在第一次月考数学试题.files/image249.gif) 轴上,
轴上,
第一次月考数学试题.files/image251.gif) 椭圆的方程为:
椭圆的方程为:第一次月考数学试题.files/image253.gif)
(2)由第一次月考数学试题.files/image255.gif) 得
得第一次月考数学试题.files/image257.gif) ,
,第一次月考数学试题.files/image259.gif)
又第一次月考数学试题.files/image261.gif)
第一次月考数学试题.files/image263.gif)
第一次月考数学试题.files/image265.gif)
19.解:
(1)连结第一次月考数学试题.files/image267.gif) 、
、第一次月考数学试题.files/image269.gif) ,则
,则第一次月考数学试题.files/image271.gif)
第一次月考数学试题.files/image273.gif)
(2)证明:连结第一次月考数学试题.files/image275.gif) 、
、第一次月考数学试题.files/image277.gif) ,则
,则第一次月考数学试题.files/image279.gif) ,
,第一次月考数学试题.files/image251.gif) PQ∥平面AA1B1B.
PQ∥平面AA1B1B.
20.解:
设数列第一次月考数学试题.files/image196.gif) 的公差为
的公差为第一次月考数学试题.files/image283.gif) ,则
,则
第一次月考数学试题.files/image285.gif) ,
,
第一次月考数学试题.files/image287.gif) ,
,
第一次月考数学试题.files/image289.gif) .????????????????????????????????????????????????????????????????????????????????????????????? 3分
.????????????????????????????????????????????????????????????????????????????????????????????? 3分
由第一次月考数学试题.files/image200.gif) 成等比数列得
成等比数列得第一次月考数学试题.files/image292.gif) ,
,
即第一次月考数学试题.files/image294.gif) ,
,
整理得第一次月考数学试题.files/image296.gif) ,
,
解得第一次月考数学试题.files/image298.gif) 或
或第一次月考数学试题.files/image300.gif) .???????????????????????????????????????????????????????????????????????????????????????????????????? 7分
.???????????????????????????????????????????????????????????????????????????????????????????????????? 7分
当第一次月考数学试题.files/image298.gif) 时,
时,第一次月考数学试题.files/image303.gif) .????????????????????????????????????????????????????????????????????????????????? 9分
.????????????????????????????????????????????????????????????????????????????????? 9分
当第一次月考数学试题.files/image300.gif) 时,
时,第一次月考数学试题.files/image306.gif) ,
,
于是第一次月考数学试题.files/image308.gif)
第一次月考数学试题.files/image310.gif) .????????????????????????????????????????????????????? 12分
.????????????????????????????????????????????????????? 12分
21.解:
(1)第一次月考数学试题.files/image312.gif) 函数
函数第一次月考数学试题.files/image204.gif) 的图像经过点
的图像经过点第一次月考数学试题.files/image206.gif)
第一次月考数学试题.files/image314.gif)
第一次月考数学试题.files/image245.gif)
(2)第一次月考数学试题.files/image312.gif) 函数为
函数为第一次月考数学试题.files/image317.gif)
第一次月考数学试题.files/image251.gif) 由
由第一次月考数学试题.files/image320.gif) 得
得第一次月考数学试题.files/image322.gif)
第一次月考数学试题.files/image324.gif)
当第一次月考数学试题.files/image326.gif) 时,
时,第一次月考数学试题.files/image320.gif) ,
,第一次月考数学试题.files/image251.gif) 函数
函数第一次月考数学试题.files/image317.gif)
第一次月考数学试题.files/image328.gif)
第一次月考数学试题.files/image251.gif) 函数为
函数为第一次月考数学试题.files/image317.gif) 的定义域为:
的定义域为:第一次月考数学试题.files/image331.gif) ;值域为:
;值域为:第一次月考数学试题.files/image333.gif)
(3)函数第一次月考数学试题.files/image317.gif) 的反函数为
的反函数为第一次月考数学试题.files/image335.gif)
第一次月考数学试题.files/image337.gif)
第一次月考数学试题.files/image251.gif) 不等式
不等式第一次月考数学试题.files/image212.gif) 为
为第一次月考数学试题.files/image341.gif)
第一次月考数学试题.files/image343.gif)
第一次月考数学试题.files/image251.gif) 不等式的解集为
不等式的解集为第一次月考数学试题.files/image345.gif)
22.证明:
(1)第一次月考数学试题.files/image312.gif) PA⊥底面ABCD
PA⊥底面ABCD 第一次月考数学试题.files/image251.gif)
第一次月考数学试题.files/image347.gif)
又第一次月考数学试题.files/image312.gif) ∠BAD=90°
∠BAD=90° 第一次月考数学试题.files/image251.gif)
第一次月考数学试题.files/image349.gif)
第一次月考数学试题.files/image251.gif)
第一次月考数学试题.files/image351.gif) 平面
平面第一次月考数学试题.files/image353.gif)
第一次月考数学试题.files/image355.gif) 是斜线
是斜线第一次月考数学试题.files/image357.gif) 在平面
在平面第一次月考数学试题.files/image353.gif) 内的射影
内的射影
第一次月考数学试题.files/image312.gif) AE⊥PD
AE⊥PD 第一次月考数学试题.files/image251.gif) BE⊥PD
BE⊥PD
(2)连结第一次月考数学试题.files/image359.gif)
第一次月考数学试题.files/image312.gif) PA⊥底面ABCD
PA⊥底面ABCD 第一次月考数学试题.files/image251.gif)
第一次月考数学试题.files/image359.gif) 是斜线
是斜线第一次月考数学试题.files/image361.gif) 在平面
在平面第一次月考数学试题.files/image363.gif) 内的射影
内的射影
第一次月考数学试题.files/image312.gif)
第一次月考数学试题.files/image365.gif)
第一次月考数学试题.files/image251.gif)
第一次月考数学试题.files/image218.gif)
(3)过第一次月考数学试题.files/image367.gif) 点作
点作第一次月考数学试题.files/image369.gif) 交
交第一次月考数学试题.files/image361.gif) 于
于第一次月考数学试题.files/image372.gif) ,连结
,连结第一次月考数学试题.files/image374.gif) ,则
,则第一次月考数学试题.files/image376.gif) (或其补角)为异面直线AE与CD所成的角。由(2)知
(或其补角)为异面直线AE与CD所成的角。由(2)知第一次月考数学试题.files/image218.gif)
第一次月考数学试题.files/image312.gif)
第一次月考数学试题.files/image365.gif)
第一次月考数学试题.files/image251.gif)
第一次月考数学试题.files/image378.gif) 平面
平面第一次月考数学试题.files/image380.gif)
又第一次月考数学试题.files/image312.gif)
第一次月考数学试题.files/image369.gif)
第一次月考数学试题.files/image251.gif)
第一次月考数学试题.files/image383.gif) 平面
平面第一次月考数学试题.files/image380.gif)
第一次月考数学试题.files/image251.gif)
第一次月考数学试题.files/image383.gif)
第一次月考数学试题.files/image374.gif)
第一次月考数学试题.files/image386.gif)
第一次月考数学试题.files/image388.gif)
第一次月考数学试题.files/image251.gif)
第一次月考数学试题.files/image390.gif)
第一次月考数学试题.files/image251.gif)
第一次月考数学试题.files/image392.gif)
第一次月考数学试题.files/image251.gif) 异面直线AE与CD所成的角为
异面直线AE与CD所成的角为第一次月考数学试题.files/image394.gif)
| 3 |
| 2 |
| 1 |
| 2 |
(1)求椭圆C的标准方程;
(2)若直线l:y=kx+m与椭圆C相交A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点,求证:直线l过定点,并求出该定点的坐标. 查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
(1)求椭圆C的方程;
(2)若直线l:y=kx+m与椭圆C相交于M、N两点(M、N不是左右顶点),且以MN为直径的圆过点A.求证:直线l过定点,并求出该定点的坐标.
椭圆![]() :
:![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() 、
、![]() ,右顶点为
,右顶点为![]() ,
,![]() 为椭圆
为椭圆![]() 上任意一点.已知
上任意一点.已知![]() 的最大值为3,最小值为2.
的最大值为3,最小值为2.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() :
:![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点(
两点(![]() 、
、![]() 不是左右顶点),且以
不是左右顶点),且以![]() 为直径的圆过点
为直径的圆过点![]() .求证:直线
.求证:直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
查看习题详情和答案>>
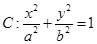
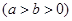 的离心率为
的离心率为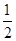 ,其左焦点到点
,其左焦点到点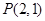 的距离为
的距离为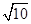 .
. 的标准方程;
的标准方程;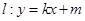 与椭圆
与椭圆 两点(
两点(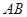 为直径的圆过椭圆
为直径的圆过椭圆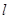 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.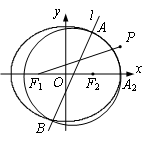

 的离心率为
的离心率为 ,其左焦点到点
,其左焦点到点 的距离为
的距离为 .
. 的标准方程;
的标准方程; 与椭圆
与椭圆 两点(
两点( 为直径的圆过椭圆
为直径的圆过椭圆 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.