摘要：NN1⊥准线于N1.则.又由抛物线的定义有
网址：http://m.1010jiajiao.com/timu_id_49251[举报]
一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有 一项是符合题目要求的。
题号
1
2
3
4
5
6
7
8
9
10
答案
二、填空题：（本大题共5个小题，每小题5分，共25分，）
11． 12. 13. 14. 15.
三、解答题：
已知抛物线y2=4x，过焦点F的直线交抛物线于M，N两点，以下命题：
①若直线MN的倾斜角为
，则|MN|=10；
②
•
=5；
③过M，N分别作准线l的垂线，垂足分别为M1，N1，则M1F⊥N1F；
④连接M0，N0并延长分别交抛物线的准线于P，0两点，则以PQ为直径的圆过焦点F．
其中真命题的序号为
查看习题详情和答案>>
①若直线MN的倾斜角为
| π |
| 4 |
②
| OM |
| ON |
③过M，N分别作准线l的垂线，垂足分别为M1，N1，则M1F⊥N1F；
④连接M0，N0并延长分别交抛物线的准线于P，0两点，则以PQ为直径的圆过焦点F．
其中真命题的序号为
③④
③④
．在直角坐标平面上，O为原点，M为动点，
，
．过点M作MM1⊥
轴于M1，过N作NN1⊥
轴于点N1，
．记点T的轨迹为曲线C，点A（5，0）、B（1，0），过点A作直线
交曲线C于两个不同的点P、Q（点Q在A与P之间）．
（Ⅰ）求曲线C的方程；
（Ⅱ）证明不存在直线，使得
；
（Ⅲ）过点P作轴的平行线与曲线C的另一交点为S，若
，证明
．
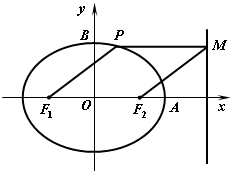如图，F1、F2为椭圆| x2 |
| a2 |
| y2 |
| b2 |
（1）若存在点P，使PF1F2M为平行四边形，求椭圆的离心率e的取值范围；
（2）若存在点P，使PF1F2M为菱形；
①求椭圆的离心率；
②设A（a，0）、B（0，b），求证：以F1A为直径的圆经过点B．