题目内容
已知抛物线y2=4x,过焦点F的直线交抛物线于M,N两点,以下命题:
①若直线MN的倾斜角为
,则|MN|=10;
②
•
=5;
③过M,N分别作准线l的垂线,垂足分别为M1,N1,则M1F⊥N1F;
④连接M0,N0并延长分别交抛物线的准线于P,0两点,则以PQ为直径的圆过焦点F.
其中真命题的序号为
①若直线MN的倾斜角为
| π |
| 4 |
②
| OM |
| ON |
③过M,N分别作准线l的垂线,垂足分别为M1,N1,则M1F⊥N1F;
④连接M0,N0并延长分别交抛物线的准线于P,0两点,则以PQ为直径的圆过焦点F.
其中真命题的序号为
③④
③④
.分析:①设直线MN的方程为y=x-1,代入y2=4x,可得|MN|=8;
②斜率不存在时,结论就不成立;
③设直线MN的方程为x=my+1代入y2=4x,验证
•
=0,即可得到结论;
④验证
•
=(-2,-
)•(-2,-
)=0,可得结论.
②斜率不存在时,结论就不成立;
③设直线MN的方程为x=my+1代入y2=4x,验证
| M1F |
| N1F |
④验证
| FP |
| FQ |
| y1 |
| x1 |
| y2 |
| x2 |
解答: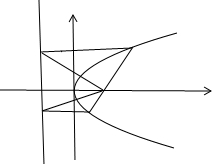 解:①设直线MN的方程为y=x-1,代入y2=4x得x2-6x+1=0
解:①设直线MN的方程为y=x-1,代入y2=4x得x2-6x+1=0
设M(x1,y1),N(x2,y2),则|MN|=
|x1-x2|=
•
=8,即①不正确;
②斜率不存在时,M(1,2),N(1,-2),
•
=1-4=-3,∴②不正确;
③设直线MN的方程为x=my+1,M(x1,y1),N(x2,y2),则
将x=my+1代入y2=4x(p>0)消去x可得y2-4my-4=0
从而有y1+y2=4m,y1y2=-4,x1x2=1
∵
=(2,-y1),
=(2,-y2),
∴
•
=(2,-y1)•(2,-y2)=0,故有M1F⊥N1F,即③正确;
④直线MO的方程为y=
x,x=-1时,y=-
,∴P(-1,-
)
同理Q(-1,-
)
∴
=(-2,-
),
=(-2,-
)
∴
•
=(-2,-
)•(-2,-
)=0,
∴以PQ为直径的圆过焦点F,即④正确
故答案为:③④.
 解:①设直线MN的方程为y=x-1,代入y2=4x得x2-6x+1=0
解:①设直线MN的方程为y=x-1,代入y2=4x得x2-6x+1=0设M(x1,y1),N(x2,y2),则|MN|=
| 2 |
| 2 |
| 36-4 |
②斜率不存在时,M(1,2),N(1,-2),
| OM |
| ON |
③设直线MN的方程为x=my+1,M(x1,y1),N(x2,y2),则
将x=my+1代入y2=4x(p>0)消去x可得y2-4my-4=0
从而有y1+y2=4m,y1y2=-4,x1x2=1
∵
| M1F |
| N1F |
∴
| M1F |
| N1F |
④直线MO的方程为y=
| y1 |
| x1 |
| y1 |
| x1 |
| y1 |
| x1 |
同理Q(-1,-
| y2 |
| x2 |
∴
| FP |
| y1 |
| x1 |
| FQ |
| y2 |
| x2 |
∴
| FP |
| FQ |
| y1 |
| x1 |
| y2 |
| x2 |
∴以PQ为直径的圆过焦点F,即④正确
故答案为:③④.
点评:本题考查直线与抛物线的位置关系,考查抛物线的性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 已知抛物线y2=4x,焦点为F,顶点为O,点P(m,n)在抛物线上移动,Q是OP的中点,M是FQ的中点.
已知抛物线y2=4x,焦点为F,顶点为O,点P(m,n)在抛物线上移动,Q是OP的中点,M是FQ的中点.