题目内容
 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)(1)已知曲线C的参数方程为
|
(2)已知不等式x+|x-2c|>1的解集为R,则正实数c的取值范围是
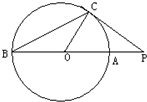
(3)如图,PC切圆O于点C,割线PAB经过圆心A,PC=4,PB=8,则S△OBC
分析:(1)把点M(5,4)的坐标代入曲线C的参数方程可得 a=1,故曲线C的参数方程为
,消去参数t,化为普通方程为(x-1)2=4y.
(2)已知不等式|x|+|x-2c|>1的解集为R,而|x|+|x-2c|表示数轴上的x对应点到0和到2c对应点的距离之和,其最小值等于正实数2c,故2c>1,从而得到c的范围.
(3)设圆的半径等于 r,则由切割线定理可得 PC2=PB•PA,求出 r 的值,可得cos∠COP,从而得到cos∠COB,利用同角三角函数的基本关系得到sin∠COB的值,由S△OBC=
r2 sin∠COB求出结果.
|
(2)已知不等式|x|+|x-2c|>1的解集为R,而|x|+|x-2c|表示数轴上的x对应点到0和到2c对应点的距离之和,其最小值等于正实数2c,故2c>1,从而得到c的范围.
(3)设圆的半径等于 r,则由切割线定理可得 PC2=PB•PA,求出 r 的值,可得cos∠COP,从而得到cos∠COB,利用同角三角函数的基本关系得到sin∠COB的值,由S△OBC=
| 1 |
| 2 |
解答:解:(1)把点M(5,4)的坐标代入曲线C的参数方程可得a=1,
故曲线C的参数方程为
,
化为普通方程为 (x-1)2=4y,
故答案为(x-1)2=4y.
(2)已知不等式|x|+|x-2c|>1的解集为R,
而|x|+|x-2c|表示数轴上的x对应点到0和到2c对应点的距离之和,
其最小值等于 正实数2c,
故2c>1,∴c>
,
故答案为c>
.
(3)设圆的半径等于r,则由切割线定理可得PC2=PB•PA,∴16=8(8-2r),
∴r=3.
故cos∠COP=
=
=
,∴cos∠COB=-
,
∴sin∠COB=
,则S△OBC=
r2 sin∠COB=
,
故答案为
.
故曲线C的参数方程为
|
化为普通方程为 (x-1)2=4y,
故答案为(x-1)2=4y.
(2)已知不等式|x|+|x-2c|>1的解集为R,
而|x|+|x-2c|表示数轴上的x对应点到0和到2c对应点的距离之和,
其最小值等于 正实数2c,
故2c>1,∴c>
| 1 |
| 2 |
故答案为c>
| 1 |
| 2 |
(3)设圆的半径等于r,则由切割线定理可得PC2=PB•PA,∴16=8(8-2r),
∴r=3.
故cos∠COP=
| OC |
| OP |
| 3 |
| 8-3 |
| 3 |
| 5 |
| 3 |
| 5 |
∴sin∠COB=
| 4 |
| 5 |
| 1 |
| 2 |
| 18 |
| 5 |
故答案为
| 18 |
| 5 |
点评:本题考查把参数方程化为普通方程的方法,绝对值的意义,绝对值不等式的解法,切割线定理,同角三角函数的基本关系,求出圆的半径,是解题的关键.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分) (2011•渭南三模)选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(2011•渭南三模)选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)