摘要：E=600E=.
网址：http://m.1010jiajiao.com/timu_id_49096[举报]
一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有 一项是符合题目要求的。
题号
1
2
3
4
5
6
7
8
9
10
答案
二、填空题：（本大题共5个小题，每小题5分，共25分，）
11． 12. 13. 14. 15.
三、解答题：
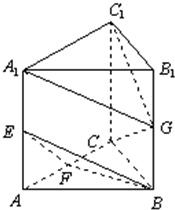16、如图，在直三棱柱ABC-A1B1C1中，∠ABC=90°，E，F，G分别是AA1，AC，BB1的中点，且CG⊥C1G．（Ⅰ）求证：CG∥平面BEF；
（Ⅱ）求证：平面BEF⊥平面A1C1G．
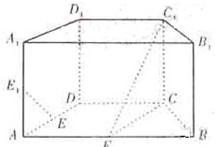如图，在直四棱柱ABCD-A1B1C1D1中，底面ABCD为等腰梯形，AB∥CD，AB=4，BC=CD=2，E、F是AA1、AB的中点．（Ⅰ）证明：直线EE1∥平面FCC1；
（Ⅱ）求二面角B-FC1-C的余弦值． 查看习题详情和答案>>
在某校组织的一次篮球定点投篮训练中，规定每人最多投3次；在A处每投进一球得3分，在B处每投进一球得2分；如果前两次得分之和超过3分即停止投篮，否则投第三次，某同学在A处的命中率q1为0.25，在B处的命中率为q2，该同学选择先在A处投一球，以后都在B处投，用ξ表示该同学投篮训练结束后所得的总分，其分布列为：
（1）求q2的值；
（2）求随机变量ξ的数学期望Eξ；
（3）试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小． 查看习题详情和答案>>
| ξ | 0 | 2 | 3 | 4 | 5 |
| p | 0.03 | 0.24 | 0.01 | 0.48 | 0.24 |
（2）求随机变量ξ的数学期望Eξ；
（3）试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小． 查看习题详情和答案>>