题目内容
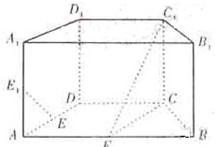 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,E、F是AA1、AB的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,E、F是AA1、AB的中点.(Ⅰ)证明:直线EE1∥平面FCC1;
(Ⅱ)求二面角B-FC1-C的余弦值.
分析:(Ⅰ)构造DM⊥CD,则以DM为x轴,DC为y轴,DD1为z轴建立空间直角坐标系,欲证直线EE1∥平面FCC1,只需证明
垂直于平面FCC1的法向量即可.其中
的坐标由点E、E1的坐标易得,而平面FCC1的法向量需设出后根据其与
、
垂直得到.
(Ⅱ)在(Ⅰ)所建立的空间直角坐标系中,平面FCC1的法向量已求得,而平面BFC1的法向量可设出后由其与
、
垂直得到,此时求出两法向量的夹角余弦值,则易得二面角B-FC1-C的余弦值.
| EE1 |
| EE1 |
| CF |
| CC1 |
(Ⅱ)在(Ⅰ)所建立的空间直角坐标系中,平面FCC1的法向量已求得,而平面BFC1的法向量可设出后由其与
| FB |
| FC1 |
解答: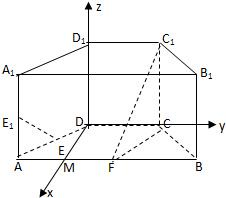 (Ⅰ)证明:因为AB=4,BC=CD=2,F是棱AB的中点,
(Ⅰ)证明:因为AB=4,BC=CD=2,F是棱AB的中点,
所以BF=BC=CF,△BCF为正三角形,
因为ABCD为等腰梯形,所以∠BAD=∠ABC=60°,
取AF的中点M,并连接DM,则DM⊥AB,所以DM⊥CD,
以DM为x轴,DC为y轴,DD1为z轴建立空间直角坐标系,
则D(0,0,0),A(
,-1,0),F(
,1,0),C(0,2,0),
C1(0,2,2),E(
,-
,0),E1(
,-1,1),
所以
=(
,-
,1),
=(
,-1,0),
=(0,0,2),
=(-
,1,2)
设平面CC1F的法向量为
=(x,y,z)
则
所以
取
=(1,
,0),
则
•
=
×1-
×
+1×0=0,
所以
⊥
,所以直线EE1∥平面FCC1.
(Ⅱ)解:
=(0,2,0),
设平面BFC1的法向量为
=(x1,y1,z1),
则
所以
,
取
=(2,0,
),
则
•
=2×1-
×0+0×
=2,|
|=
=2,
|
|=
=
,
所以cos?
,
?=
=
=
,
由图可知二面角B-FC1-C为锐角,所以二面角B-FC1-C的余弦值为
.
 (Ⅰ)证明:因为AB=4,BC=CD=2,F是棱AB的中点,
(Ⅰ)证明:因为AB=4,BC=CD=2,F是棱AB的中点,所以BF=BC=CF,△BCF为正三角形,
因为ABCD为等腰梯形,所以∠BAD=∠ABC=60°,
取AF的中点M,并连接DM,则DM⊥AB,所以DM⊥CD,
以DM为x轴,DC为y轴,DD1为z轴建立空间直角坐标系,
则D(0,0,0),A(
| 3 |
| 3 |
C1(0,2,2),E(
| ||
| 2 |
| 1 |
| 2 |
| 3 |
所以
| EE1 |
| ||
| 2 |
| 1 |
| 2 |
| CF |
| 3 |
| CC1 |
| FC1 |
| 3 |
设平面CC1F的法向量为
| n |
则
|
|
取
| n |
| 3 |
则
| n |
| EE1 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
所以
| n |
| EE1 |
(Ⅱ)解:
| FB |
设平面BFC1的法向量为
| n1 |
则
|
|
取
| n1 |
| 3 |
则
| n |
| n1 |
| 3 |
| 3 |
| n |
1+(
|
|
| n1 |
22+0+(
|
| 7 |
所以cos?
| n |
| n1 |
| ||||
|
|
| 2 | ||
2×
|
| ||
| 7 |
由图可知二面角B-FC1-C为锐角,所以二面角B-FC1-C的余弦值为
| ||
| 7 |
点评:本题主要考查向量法解决空间问题.

练习册系列答案
相关题目
 18、如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点,F为AB的中点.证明:
18、如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点,F为AB的中点.证明: 18、如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点.
18、如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点. 15、如图,在直四棱柱ABCD-A1B1C1D1中,A1C1⊥B1D1,E,F分别是AB,BC的中点.
15、如图,在直四棱柱ABCD-A1B1C1D1中,A1C1⊥B1D1,E,F分别是AB,BC的中点. 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1,F分别是棱AD,AA1,AB的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1,F分别是棱AD,AA1,AB的中点. (2010•抚州模拟)如图,在直四棱柱ABCD-A1B1C1D1中,AB=BC,∠ABC=60°,BB1=BC=2,M为BC中点,点N在CC1上.
(2010•抚州模拟)如图,在直四棱柱ABCD-A1B1C1D1中,AB=BC,∠ABC=60°,BB1=BC=2,M为BC中点,点N在CC1上.