题目内容
函数y=
的图象大致为（ ）
| ex+e-x |
| ex-e-x |
A、 |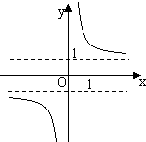
B、 |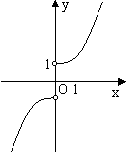
C、 |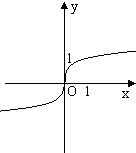
D、 |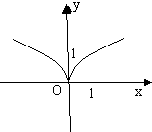
分析：欲判断图象大致图象，可从函数的定义域{x|x≠0}方面考虑，还可从函数的单调性（在函数当x＞0时函数为减函数）方面进行考虑即可．
解答：解析：函数有意义，需使ex-e-x≠0，
其定义域为{x|x≠0}，排除C，D，
又因为y=
=
=1+
，
所以当x＞0时函数为减函数，故选A
答案：A．
其定义域为{x|x≠0}，排除C，D，
又因为y=
| ex+e-x |
| ex-e-x |
| e2x+1 |
| e2x-1 |
| 2 |
| e2x-1 |
所以当x＞0时函数为减函数，故选A
答案：A．
点评：本题考查了函数的图象以及函数的定义域、值域、单调性等性质．本题的难点在于给出的函数比较复杂，需要对其先变形，再在定义域内对其进行考查其余的性质．
练习册系列答案
名校课堂系列答案
相关题目
(ex+e-x)的导数是( ) 
(ex-e-x) B.
(ex+e-x)