题目内容
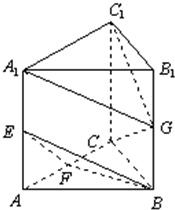 16、如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,E,F,G分别是AA1,AC,BB1的中点,且CG⊥C1G.
16、如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,E,F,G分别是AA1,AC,BB1的中点,且CG⊥C1G.(Ⅰ)求证:CG∥平面BEF;
(Ⅱ)求证:平面BEF⊥平面A1C1G.
分析:(Ⅰ)连接AG交BE于D,连接DF,EG,要证CG∥平面BEF,只需证明直线CG平行平面BEF内的直线DF即可;
(Ⅱ)要证平面BEF⊥平面A1C1G,只需证明平面BEF的直线DF,垂直平面A1C1G内的两条相交直线A1C1、C1G,即可证明DF⊥平面A1C1G,从而证明平面BEF⊥平面A1C1G
(Ⅱ)要证平面BEF⊥平面A1C1G,只需证明平面BEF的直线DF,垂直平面A1C1G内的两条相交直线A1C1、C1G,即可证明DF⊥平面A1C1G,从而证明平面BEF⊥平面A1C1G
解答:证明:(Ⅰ)连接AG交BE于D,连接DF,EG.
∵E,G分别是AA1,BB1的中点,
∴AE∥BG且AE=BG,
∴四边形AEGB是矩形.
∴D是AG的中点(3分)
又∵F是AC的中点,
∴DF∥CG(5分)
则由DF?面BEF,CG?面BEF,得CG∥面BEF(7分)
(注:利用面面平行来证明的,类似给分)
(Ⅱ)∵在直三棱柱ABC-AB1C1中,C1C⊥地面A1B1C1,
∴C1C⊥A1C1.
又∵∠A1B1C1=∠ABC=90O,即C1B1⊥A1C1,
∴A1C1⊥面B1C1CB(9分)
而CG?面B1C1CB,
∴A1C1⊥CG(11分)
又CG⊥C1G,
由(Ⅰ)DF∥CG,
∴A1C1⊥DF,DF⊥C1G
∴DF⊥平面A1C1G(13分)
∵DF?平面BEF,
∴平面BEF⊥平面A1C1G.(14分)
∵E,G分别是AA1,BB1的中点,
∴AE∥BG且AE=BG,
∴四边形AEGB是矩形.
∴D是AG的中点(3分)
又∵F是AC的中点,
∴DF∥CG(5分)
则由DF?面BEF,CG?面BEF,得CG∥面BEF(7分)
(注:利用面面平行来证明的,类似给分)
(Ⅱ)∵在直三棱柱ABC-AB1C1中,C1C⊥地面A1B1C1,
∴C1C⊥A1C1.
又∵∠A1B1C1=∠ABC=90O,即C1B1⊥A1C1,
∴A1C1⊥面B1C1CB(9分)
而CG?面B1C1CB,
∴A1C1⊥CG(11分)
又CG⊥C1G,
由(Ⅰ)DF∥CG,
∴A1C1⊥DF,DF⊥C1G
∴DF⊥平面A1C1G(13分)
∵DF?平面BEF,
∴平面BEF⊥平面A1C1G.(14分)
点评:本题考查直线与平面的平行的判定 平面与平面垂直的判定,开心逻辑思维能力 空间想象能力,是中档题.

练习册系列答案
相关题目




