摘要:7 空间向量基本定理:
网址:http://m.1010jiajiao.com/timu_id_490556[举报]
由空间向量基本定理可知,空间任意向量
可由三个不共面的向量
,
,
唯一确定地表示为
=x
+y
+z
,则称(x,y,z)为基底<
,
,
>下的广义坐标.特别地,当<
,
,
>为单位正交基底时,(x,y,z)为直角坐标.设
,
,
分别为直角坐标中x,y,z正方向上的单位向量,则空间直角坐标(1,2,3)在基底<
+
,
-
,
>下的广义坐标为
查看习题详情和答案>>
| p |
| a |
| b |
| c |
| p |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| i |
| j |
| k |
| i |
| j |
| i |
| j |
| k |
(
,-
,3)
| 3 |
| 2 |
| 1 |
| 2 |
(
,-
,3)
.| 3 |
| 2 |
| 1 |
| 2 |
由空间向量基本定理可知,空间任意向量
可由三个不共面的向量
,
,
唯一确定地表示为
=x
+y
+z
,则称(x,y,z)为基底<
,
,
>下的广义坐标.特别地,当<
,
,
>为单位正交基底时,(x,y,z)为直角坐标.设
,
,
分别为直角坐标中x,y,z正方向上的单位向量,则空间直角坐标(1,2,3)在基底<
+
,
-
,
>下的广义坐标为______.
查看习题详情和答案>>
| p |
| a |
| b |
| c |
| p |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| i |
| j |
| k |
| i |
| j |
| i |
| j |
| k |
由空间向量基本定理可知,空间任意向量 可由三个不共面的向量
可由三个不共面的向量 唯一确定地表示为
唯一确定地表示为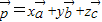 ,则称(x,y,z)为基底
,则称(x,y,z)为基底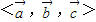 下的广义坐标.特别地,当
下的广义坐标.特别地,当 为单位正交基底时,(x,y,z)为直角坐标.设
为单位正交基底时,(x,y,z)为直角坐标.设 分别为直角坐标中x,y,z正方向上的单位向量,则空间直角坐标(1,2,3)在基底
分别为直角坐标中x,y,z正方向上的单位向量,则空间直角坐标(1,2,3)在基底 下的广义坐标为 .
查看习题详情和答案>>
下的广义坐标为 .
查看习题详情和答案>>
 可由三个不共面的向量
可由三个不共面的向量 唯一确定地表示为
唯一确定地表示为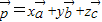 ,则称(x,y,z)为基底
,则称(x,y,z)为基底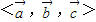 下的广义坐标.特别地,当
下的广义坐标.特别地,当 为单位正交基底时,(x,y,z)为直角坐标.设
为单位正交基底时,(x,y,z)为直角坐标.设 分别为直角坐标中x,y,z正方向上的单位向量,则空间直角坐标(1,2,3)在基底
分别为直角坐标中x,y,z正方向上的单位向量,则空间直角坐标(1,2,3)在基底 下的广义坐标为 .
查看习题详情和答案>>
下的广义坐标为 .
查看习题详情和答案>>
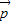 可由三个不共面的向量
可由三个不共面的向量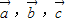 唯一确定地表示为
唯一确定地表示为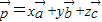 ,则称(x,y,z)为基底
,则称(x,y,z)为基底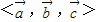 下的广义坐标.特别地,当
下的广义坐标.特别地,当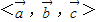 为单位正交基底时,(x,y,z)为直角坐标.设
为单位正交基底时,(x,y,z)为直角坐标.设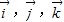 分别为直角坐标中x,y,z正方向上的单位向量,则空间直角坐标(1,2,3)在基底
分别为直角坐标中x,y,z正方向上的单位向量,则空间直角坐标(1,2,3)在基底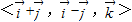 下的广义坐标为 .
下的广义坐标为 . 是两个不共线的非零向量.
是两个不共线的非零向量. =
= ,
, =
= ,
, =
= ,求证:A,B,D三点共线;
,求证:A,B,D三点共线; 和
和 共线. (本小题满分13分)
共线. (本小题满分13分) =(
=( =
= 得到共线问题。
得到共线问题。 ,使得
,使得 ,结合平面向量基本定理得到参数的值。
,结合平面向量基本定理得到参数的值。 ……………5分
……………5分 ∴A,B,D三点共线 ……………7分
∴A,B,D三点共线 ……………7分 ……………12分
……………12分