题目内容
由空间向量基本定理可知,空间任意向量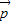 可由三个不共面的向量
可由三个不共面的向量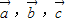 唯一确定地表示为
唯一确定地表示为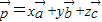 ,则称(x,y,z)为基底
,则称(x,y,z)为基底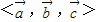 下的广义坐标.特别地,当
下的广义坐标.特别地,当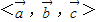 为单位正交基底时,(x,y,z)为直角坐标.设
为单位正交基底时,(x,y,z)为直角坐标.设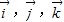 分别为直角坐标中x,y,z正方向上的单位向量,则空间直角坐标(1,2,3)在基底
分别为直角坐标中x,y,z正方向上的单位向量,则空间直角坐标(1,2,3)在基底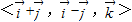 下的广义坐标为 .
下的广义坐标为 .
【答案】分析:欲求空间直角坐标(1,2,3)在基底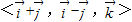 下的广义坐标,即对于平面向量
下的广义坐标,即对于平面向量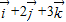 ,存在唯一的实数对p,q,r,使得
,存在唯一的实数对p,q,r,使得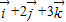 =
=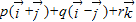 ,据此列出关于p,q,r的方程求解即可.
,据此列出关于p,q,r的方程求解即可.
解答:解:根据平面向量基本定理,空间直角坐标(1,2,3)对应的向量为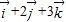 ,
,
由于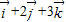 =
=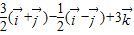 ,
,
则空间直角坐标(1,2,3)在基底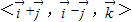 下的广义坐标为(
下的广义坐标为(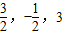 )
)
故答案为:(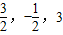 ).
).
点评:本题考查平面向量正交分解的应用,考查一个新定义问题,考查学生的理解能力和应变能力,是一个比较好的题目.
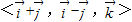 下的广义坐标,即对于平面向量
下的广义坐标,即对于平面向量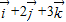 ,存在唯一的实数对p,q,r,使得
,存在唯一的实数对p,q,r,使得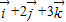 =
=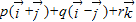 ,据此列出关于p,q,r的方程求解即可.
,据此列出关于p,q,r的方程求解即可.解答:解:根据平面向量基本定理,空间直角坐标(1,2,3)对应的向量为
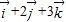 ,
,由于
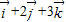 =
=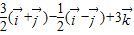 ,
,则空间直角坐标(1,2,3)在基底
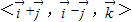 下的广义坐标为(
下的广义坐标为(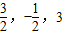 )
)故答案为:(
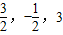 ).
).点评:本题考查平面向量正交分解的应用,考查一个新定义问题,考查学生的理解能力和应变能力,是一个比较好的题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 可由三个不共面的向量
可由三个不共面的向量 唯一确定地表示为
唯一确定地表示为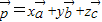 ,则称(x,y,z)为基底
,则称(x,y,z)为基底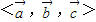 下的广义坐标.特别地,当
下的广义坐标.特别地,当 为单位正交基底时,(x,y,z)为直角坐标.设
为单位正交基底时,(x,y,z)为直角坐标.设 分别为直角坐标中x,y,z正方向上的单位向量,则空间直角坐标(1,2,3)在基底
分别为直角坐标中x,y,z正方向上的单位向量,则空间直角坐标(1,2,3)在基底 下的广义坐标为 .
下的广义坐标为 .