摘要：②BN==1/2
网址：http://m.1010jiajiao.com/timu_id_490511[举报]
（理）数列{an}，若对任意的k∈N*，满足
=q1，
=q2
是常数且不相等），则称数列{an}为“跳跃等比数列”，则下列关于“跳跃等比数列”的命题：
（1）若数列{an}为“跳跃等比数列”，则满足bk=a2k•a2k-1（k∈N*）的数列{bn}是等比数列；
（2）若数列{an}为“跳跃等比数列”，则满足bk=
(k∈N*)的数列{bn}是等比数列；
（3）若数列{an}为等比数列，则数列{（-1）nan}是“跳跃等比数列”；
（4）若数列{an}为等比数列，则满足bn=
(k∈N*)的数列{bn}是“跳跃等比数列”；
（5）若数列{an}和{bn}都是“跳跃等比数列”，则数列{an•bn}也是“跳跃等比数列”；其中正确的命题个数为（ ）
| a2k+1 |
| a2k-1 |
| a2k+2 |
| a2k |
|
（1）若数列{an}为“跳跃等比数列”，则满足bk=a2k•a2k-1（k∈N*）的数列{bn}是等比数列；
（2）若数列{an}为“跳跃等比数列”，则满足bk=
| a2k |
| a2k-1 |
（3）若数列{an}为等比数列，则数列{（-1）nan}是“跳跃等比数列”；
（4）若数列{an}为等比数列，则满足bn=
|
（5）若数列{an}和{bn}都是“跳跃等比数列”，则数列{an•bn}也是“跳跃等比数列”；其中正确的命题个数为（ ）
查看习题详情和答案>>
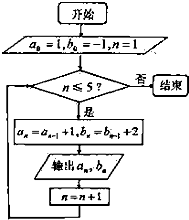（2013•湛江一模）已知函数f（x）=lg（x2-anx+bn），其中an，bn的值由如图的程序框图产生，运行该程序所得的函数中，定义域为R的有（ ）