摘要：.满足②4分
网址：http://m.1010jiajiao.com/timu_id_486484[举报]
设满足以下两个条件的有穷数列a1，a2，…，an为n（n=2，3，4，…，）阶“期待数列”：①a1+a2+a3+…+an=0；②|a1|+|a2|+|a3|+…+|an|=1．
（1）分别写出一个单调递增的3阶和4阶“期待数列”；
（2）若某2k+1（k∈N*）阶“期待数列”是等差数列，求该数列的通项公式．
查看习题详情和答案>>
（1）分别写出一个单调递增的3阶和4阶“期待数列”；
（2）若某2k+1（k∈N*）阶“期待数列”是等差数列，求该数列的通项公式．
轴上，长轴长等于12，离心率等于
；椭圆经过点
；椭圆的一个焦点到长轴两端点的距离分别为10和4.数列
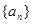，满足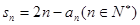
（1）求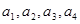
，并猜想通项公式
。
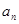（2）用数学归纳法证明（1）中的猜想。
【解析】本试题主要考查了数列的通项公式求解，并用数学归纳法加以证明。第一问利用递推关系式得到
，
，
，
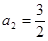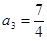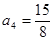，并猜想通项公式
第二问中，用数学归纳法证明（1）中的猜想。
①对n=1，等式成立。
②假设n=k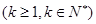
时，
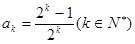成立，
那么当n=k+1时，
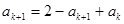，所以当n=k+1时结论成立可证。
数列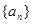，满足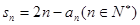
（1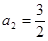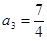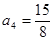），，，并猜想通项公。 …4分
（2）用数学归纳法证明（1）中的猜想。①对n=1，等式成立。 …5分
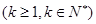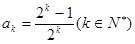②假设n=k时，成立，
那么当n=k+1时，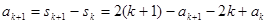
，
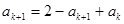……9分
所以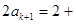
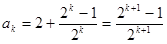
所以当n=k+1时结论成立 ……11分
由①②知，猜想对一切自然数n均成立
查看习题详情和答案>>
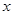轴上，长轴长等于12，离心率等于
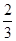；椭圆经过点
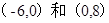；椭圆的一个焦点到长轴两端点的距离分别为10和4.