题目内容
设满足以下两个条件的有穷数列a1,a2,…,an为n(n=2,3,4,…,)阶“期待数列”:①a1+a2+a3+…+an=0;②|a1|+|a2|+|a3|+…+|an|=1.
(1)分别写出一个单调递增的3阶和4阶“期待数列”;
(2)若某2k+1(k∈N*)阶“期待数列”是等差数列,求该数列的通项公式.
(1)分别写出一个单调递增的3阶和4阶“期待数列”;
(2)若某2k+1(k∈N*)阶“期待数列”是等差数列,求该数列的通项公式.
分析:(1)利用新定义直接利用等差数列,写出一个单调递增的3阶和4阶“期待数列”;
(2)利用某2k+1(k∈N*)阶“期待数列”是等差数列,通过公差为0,大于0.小于0,分别求解该数列的通项公式.
(2)利用某2k+1(k∈N*)阶“期待数列”是等差数列,通过公差为0,大于0.小于0,分别求解该数列的通项公式.
解答:解:(1)数列-
,0,
为三阶期待数列…(1分)
数列-
,-
,
,
为四阶期待数列,…..…..(3分)(其它答案酌情给分)
(2)设等差数列a1,a2,a3,…,a2k+1(k≥1)的公差为d,
∵a1+a2+a3+…+a2k+1=0,
∴(2k+1)a1+
=0,
所以a1+kd=0,
即ak+1=0,∴ak+2=d,…(4分)
当d=0时,与期待数列的条件①②矛盾,…(5分)
当d>0时,据期待数列的条件①②得:a k+2+a k+3+…+a 2k+1=
,
∴kd+
d=
,即d=
由ak+1=0得 a 1+k•
=0,即 a1=-
,
∴an=-
+(n-1)
=
-
(n∈N*,n≤2k+1).…(7分)
当d<0时,
同理可得kd+
d=-
,即d=-
由ak+1=0得a1-k•
=0,即a1=
,
∴an=
-(n-1)
=-
+
(n∈N*,n≤2n+1).…(12分)
| 1 |
| 2 |
| 1 |
| 2 |
数列-
| 3 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| 3 |
| 8 |
(2)设等差数列a1,a2,a3,…,a2k+1(k≥1)的公差为d,
∵a1+a2+a3+…+a2k+1=0,
∴(2k+1)a1+
| 2k(2k+1)d |
| 2 |
所以a1+kd=0,
即ak+1=0,∴ak+2=d,…(4分)
当d=0时,与期待数列的条件①②矛盾,…(5分)
当d>0时,据期待数列的条件①②得:a k+2+a k+3+…+a 2k+1=
| 1 |
| 2 |
∴kd+
| k(k-1) |
| 2 |
| 1 |
| 2 |
| 1 |
| k(k+1) |
由ak+1=0得 a 1+k•
| 1 |
| k(k+1) |
| 1 |
| k+1 |
∴an=-
| 1 |
| k+1 |
| 1 |
| k(k+1) |
| n |
| k(k+1) |
| 1 |
| k |
当d<0时,
同理可得kd+
| k(k-1) |
| 2 |
| 1 |
| 2 |
| 1 |
| k(k+1) |
由ak+1=0得a1-k•
| 1 |
| k(k+1) |
| 1 |
| k+1 |
∴an=
| 1 |
| k+1 |
| 1 |
| k(k+1) |
| n |
| k(k+1) |
| 1 |
| k |
点评:本题考查新数列新定义的应用,求数列的通项公式的方法,考查分析问题解决问题的能力,难度中,考查计算能力.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目

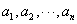 为
为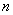
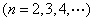 阶“期待数列”:
阶“期待数列”: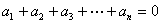 ;②
;②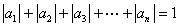 .
.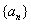 为
为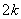 (
(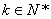 )阶“期待数列”,求公比
)阶“期待数列”,求公比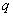 ;
;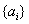 的前
的前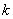 项和为
项和为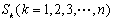 :
: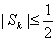 ;
;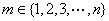 使
使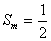 ,试问数列
,试问数列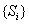 能否为
能否为