摘要:(2)由解得为所求的系数最大的项.
网址:http://m.1010jiajiao.com/timu_id_485344[举报]
已知函数 。
。
(1)求函数的最小正周期和最大值;
(2)求函数的增区间;
(3)函数的图象可以由函数 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
【解析】本试题考查了三角函数的图像与性质的运用。第一问中,利用 可知函数的周期为
可知函数的周期为 ,最大值为
,最大值为 。
。
第二问中,函数 的单调区间与函数
的单调区间与函数 的单调区间相同。故当
的单调区间相同。故当 ,解得x的范围即为所求的区间。
,解得x的范围即为所求的区间。
第三问中,利用图像将 的图象先向右平移
的图象先向右平移 个单位长度,再把横坐标缩短为原来的
个单位长度,再把横坐标缩短为原来的 (纵坐标不变),然后把纵坐标伸长为原来的
(纵坐标不变),然后把纵坐标伸长为原来的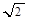 倍(横坐标不变),再向上平移1个单位即可。
倍(横坐标不变),再向上平移1个单位即可。
解:(1)函数 的最小正周期为
的最小正周期为 ,最大值为
,最大值为 。
。
(2)函数 的单调区间与函数
的单调区间与函数 的单调区间相同。
的单调区间相同。
 即
即
 所求的增区间为
所求的增区间为 ,
,
 即
即
 所求的减区间为
所求的减区间为 ,
, 。
。
(3)将 的图象先向右平移
的图象先向右平移 个单位长度,再把横坐标缩短为原来的
个单位长度,再把横坐标缩短为原来的 (纵坐标不变),然后把纵坐标伸长为原来的
(纵坐标不变),然后把纵坐标伸长为原来的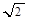 倍(横坐标不变),再向上平移1个单位即可。
倍(横坐标不变),再向上平移1个单位即可。
查看习题详情和答案>>
(1)设a>0,解关于y的不等式y2-2(
+
)y+1≤0;
(2)对于任意给定的a≥2,由(1)所确定的y解集(用区间表示)记为I(a),我们规定:区间[m,n]的长度为n-m.如果I(a)的长度为r(a),试求当a取什么值时,r(a)取得最小值,并求r(a)的最小值及此时的I(a).
查看习题详情和答案>>
| a |
| 1 | ||
|
(2)对于任意给定的a≥2,由(1)所确定的y解集(用区间表示)记为I(a),我们规定:区间[m,n]的长度为n-m.如果I(a)的长度为r(a),试求当a取什么值时,r(a)取得最小值,并求r(a)的最小值及此时的I(a).
阅读问题:“已知曲线C1:xy+2x+2=0与曲线C2:x-xy+y+a=0有两个公共点,求经过这两个公共点的直线方程.”
解:曲线C1方程与曲线C2方程相加得3x+y+2+a=0,这就是所求的直线方程.
若曲线x2+2y2=1与曲线3y2=ax+b有3个公共点,且它们不共线,则经过这3个公共点得圆的方程是
查看习题详情和答案>>
解:曲线C1方程与曲线C2方程相加得3x+y+2+a=0,这就是所求的直线方程.
若曲线x2+2y2=1与曲线3y2=ax+b有3个公共点,且它们不共线,则经过这3个公共点得圆的方程是
3x2+3y2+ax+b-3=0
3x2+3y2+ax+b-3=0
.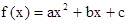 满足:
满足: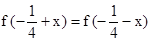 ,且
,且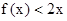 的
的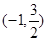
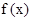 的解析式;
的解析式;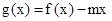
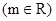 ,若
,若 在
在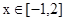 上的最小值为-4,求
上的最小值为-4,求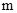 的值.
的值.