网址:http://m.1010jiajiao.com/timu_id_484960[举报]
(1)当n=1时,S1=a1显然成立;
(2)假设当n=k时,公式成立,即Sk=ka1+![]() ,
,
当n=k+1时,Sk+1 =a1+a2+…+ak+ak+1 =a1+(a1+d)+(a1+2d)+…+[a1+(k-1)d]+(a1+kd)=(k+1)a1+(d+2d+…+kd)
=(k+1)a1+![]() d=(k+1)a1+
d=(k+1)a1+![]() d,
d,
∴n=k+1时公式成立.
由(1)(2)知,对n∈N*时,公式都成立.
以上证明错误的是( )
A.当n取第一个值1时,证明不对
B.归纳假设的写法不对
C.从n=k到n=k+1时的推理中未用归纳假设
D.从n=k到n=k+1时的推理有错误
查看习题详情和答案>>数列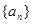 ,满足
,满足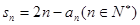
(1)求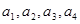 ,并猜想通项公式
,并猜想通项公式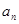 。
。
(2)用数学归纳法证明(1)中的猜想。
【解析】本试题主要考查了数列的通项公式求解,并用数学归纳法加以证明。第一问利用递推关系式得到 ,
,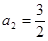 ,
,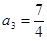 ,
,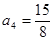 ,并猜想通项公式
,并猜想通项公式
第二问中,用数学归纳法证明(1)中的猜想。
①对n=1, 等式成立。
等式成立。
②假设n=k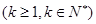 时,
时,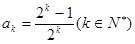 成立,
成立,
那么当n=k+1时,
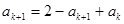 ,所以当n=k+1时结论成立可证。
,所以当n=k+1时结论成立可证。
数列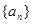 ,满足
,满足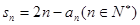
(1) ,
,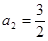 ,
,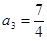 ,
,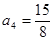 并猜想通项公
并猜想通项公 。 …4分
。 …4分
(2)用数学归纳法证明(1)中的猜想。①对n=1, 等式成立。 …5分
等式成立。 …5分
②假设n=k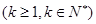 时,
时,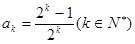 成立,
成立,
那么当n=k+1时,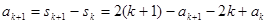
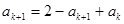 ,
……9分
,
……9分
所以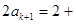
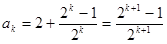
所以当n=k+1时结论成立 ……11分
由①②知,猜想对一切自然数n 均成立
均成立
查看习题详情和答案>>
在平面直角坐标系中,已知三个点列![]() ,其中
,其中![]() ,满足向量
,满足向量![]() 与向量
与向量![]() 平行,并且点列
平行,并且点列![]() 在斜率为6的同一直线上,
在斜率为6的同一直线上,![]() 。
。
证明:数列![]() 是等差数列;
是等差数列;
试用![]() 与
与![]() 表示
表示![]() ;
;
设![]() ,是否存在这样的实数
,是否存在这样的实数![]() ,使得在
,使得在![]() 与
与![]() 两项中至少有一项是数列
两项中至少有一项是数列![]() 的最小项?若存在,请求出实数
的最小项?若存在,请求出实数![]() 的取值范围;若不存在,请说明理由;
的取值范围;若不存在,请说明理由;
若![]() ,对于区间[0,1]上的任意l,总存在不小于2的自然数k,当n??k时,
,对于区间[0,1]上的任意l,总存在不小于2的自然数k,当n??k时,![]() 恒成立,求k的最小值.
恒成立,求k的最小值.
 是等差数列,其前n项和为Sn,
是等差数列,其前n项和为Sn, 是等比数列,且
是等比数列,且 ,
, .
. ,
, ,证明
,证明 (
( 的公差为d,等比数列
的公差为d,等比数列 的公比为q.
的公比为q. ,得
,得 ,
, ,
, .
. ,解得
,解得
 ,
, ,
, .
. ①
① ②
②



 ,
,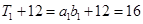 ,
, ,故等式成立.
,故等式成立. ,则当n=k+1时,有:
,则当n=k+1时,有:





 ,因此n=k+1时等式也成立
,因此n=k+1时等式也成立