题目内容
在平面直角坐标系中，已知三个点列
，其中
，满足向量
与向量
平行，并且点列
在斜率为6的同一直线上，
。
证明：数列
是等差数列；
试用
与
表示
；
设
，是否存在这样的实数
，使得在
与
两项中至少有一项是数列
的最小项？若存在，请求出实数的取值范围；若不存在，请说明理由；
若
，对于区间[0，1]上的任意l，总存在不小于2的自然数k，当n??k时，
恒成立，求k的最小值.
（1）见解析（2）
（3）
（4）4
解析:
（1）因为点列
在斜率为6，
所以
，即
，所以，数列
是等差数列. 3分
(2) 
，
，
因为
//
所以
5分
又
，
，
，
，
，
????????????????
，
将以上等式相加得
，
所以. 8分
(3) 
10分
若存在这样的实数
，使得在
与
两项中至少有一项是数列
的最小项，
则
，解得. 13分
(4) 
由
，
，
即
， 15分
记
，则有
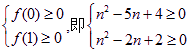，解得n??4或n??1，但由于n??2，所以n??4，kmin=4. 18分
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目