摘要:解:(1)∵.∴.∴切线l的方程为:.即材.
网址:http://m.1010jiajiao.com/timu_id_484950[举报]
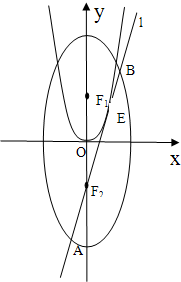 如图,已知椭圆C:
如图,已知椭圆C:| x2 |
| b2 |
| y2 |
| a2 |
| F2B |
| AF2 |
(1)求证:切线l的斜率为定值;
(2)若动点T满足:
| ET |
| EF1 |
| EF2 |
| 1 |
| 2 |
| ET |
| OT |
| 5 |
| 4 |
(3)当λ∈[2,4]时,求椭圆离心率e的取值范围.
网址:http://m.1010jiajiao.com/timu_id_484950[举报]
 如图,已知椭圆C:
如图,已知椭圆C:| x2 |
| b2 |
| y2 |
| a2 |
| F2B |
| AF2 |
| ET |
| EF1 |
| EF2 |
| 1 |
| 2 |
| ET |
| OT |
| 5 |
| 4 |