Question

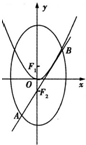如图所示，椭圆C：

x2

b2

+

y2

a2

=1(a＞b＞0)的焦点为F₁（0，c），F₂（0，-c）（c＞0），抛物线x²=2py（p＞0）的焦点与F₁重合，过F₂的直线l与抛物线P相切，切点在第一象限，且与椭圆C相交于A，B两点，且

F2B

=λ

AF2

．
（1）求证：切线l的斜率为定值；
（2）当λ∈[2，4]时，求椭圆的离心率e的取值范围．

Answer 1

分析：（1）设过F₂的直线l的方程为y+c=kx，与抛物线联立，利用过F₂的直线l与抛物线P相切，切点E在第一象限，可得结论；
（2）由（1），可得直线l的方程为y=x-c，代入椭圆方程，利用韦达定理及向量知识，确定离心率的表达式，即可得到结论．

解答：（1）证明：∵椭圆C：

x2

b2

+

y2

a2

=1(a＞b＞0)的焦点为F₁（0，c），F₂（0，-c）（c＞0），抛物线P：x²=2py（p＞0）的焦点与F₁重合，
∴

p

2

=c，∴抛物线P：x²=4cy．
设过F₂的直线l的方程为y+c=kx，与抛物线联立，可得x²-4kcx+4c²=0，
∵过F₂的直线l与抛物线P相切，切点E在第一象限，
∴△=16k²c²-16c²=0，k＞0
∴k=1，即切线l的斜率为定值；
（2）解：由（1），可得直线l的方程为y=x-c，代入椭圆方程可得（a²+b²）x²-2b²cx+b²c²-a²b²=0
设A（x₁，y₁），B（x₂，y₂），则x1+x2=

2b2c

a2+b2

①，x1x2=

b2(c2-a2)

a2+b2

②
∵

F2B

=λ

AF2

∴x₂=-λx₁③
由①②③可得

e2

2-e2

=

1

4

(λ+

1

λ

)-

1

2

∵f（λ）=

1

4

(λ+

1

λ

)-

1

2

，当λ∈[2，4]时，单调递增，
∴f（λ）∈[

1

8

，

9

16

]
∴

1

8

≤

e2

2-e2

≤

9

16

∵0＜e＜1
∴椭圆的离心率e的取值范围是[

2

3

，

3 2

5

]．

点评：本题考查切线斜率为定值的求法，考查椭圆离心率取值范围的求法，考查学生分析解决问题的能力，属于中档题．