网址:http://m.1010jiajiao.com/timu_id_484833[举报]
| 1 |
| x+a |
学生甲:在一个坐标系内作出函数f(x)=
| 1 |
| x+a |
学生乙:在坐标平面内作出函数f(x)=x+a+
| 1 |
| x+a |
则以下对上述两位同学的解题方法和结论的判断都正确的是( )
某港口海水的深度 (米)是时间
(米)是时间 (时)(
(时)( )的函数,记为:
)的函数,记为:
已知某日海水深度的数据如下:
|
|
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
|
10.0 |
13.0 |
9.9 |
7.0 |
10.0 |
13.0 |
10.1 |
7.0 |
10.0 |
经长期观察, 的曲线可近似地看成函数
的曲线可近似地看成函数 的图象
的图象
(I)试根据以上数据,求出函数 的振幅、最小正周期和表达式;
的振幅、最小正周期和表达式;
(II)一般情况下,船舶航行时,船底离海底的距离为 米或
米或 米以上时认为是安全的(船舶停靠时,船底只需不碰海底即可)。某船吃水深度(船底离水面的距离)为
米以上时认为是安全的(船舶停靠时,船底只需不碰海底即可)。某船吃水深度(船底离水面的距离)为 米,如果该船希望在同一天内安全进出港,请问,它至多能在港内停留多长时间(忽略进出港所需时间)
米,如果该船希望在同一天内安全进出港,请问,它至多能在港内停留多长时间(忽略进出港所需时间)
【解析】第一问中利用三角函数的最小正周期为:
T=12 振幅:A=3,b=10,

 第二问中,该船安全进出港,需满足:
第二问中,该船安全进出港,需满足: 即:
即:
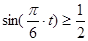 ∴
∴ 又
又  ,可解得结论为
,可解得结论为 或
或 得到。
得到。
查看习题详情和答案>>
 >0恒成立,求实数a的取值范围.”有两位同学用数形结合的方法分别提出了自己的解题思路和答案:
>0恒成立,求实数a的取值范围.”有两位同学用数形结合的方法分别提出了自己的解题思路和答案:学生甲:在一个坐标系内作出函数
 和g(x)=-x+a的大致图象,随着a的变化,要求f(x)的图象再y轴右侧的部分恒在g(x)的上方.可解得a的取值范围是[0,+∞]
和g(x)=-x+a的大致图象,随着a的变化,要求f(x)的图象再y轴右侧的部分恒在g(x)的上方.可解得a的取值范围是[0,+∞]学生乙:在坐标平面内作出函数
 的大致图象,随着a的变化,要求f(x)的图象再y轴右侧的部分恒在直线y=2a的上方.可解得a的取值范围是[0,1].
的大致图象,随着a的变化,要求f(x)的图象再y轴右侧的部分恒在直线y=2a的上方.可解得a的取值范围是[0,1].则以下对上述两位同学的解题方法和结论的判断都正确的是( )
A.甲同学方法正确,结论错误
B.乙同学方法正确,结论错误
C.甲同学方法正确,结论正确
D.乙同学方法错误,结论正确
查看习题详情和答案>>
现有问题:“对任意x>0,不等式x-a+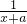 >0恒成立,求实数a的取值范围.”有两位同学用数形结合的方法分别提出了自己的解题思路和答案:
>0恒成立,求实数a的取值范围.”有两位同学用数形结合的方法分别提出了自己的解题思路和答案:
学生甲:在一个坐标系内作出函数 和g(x)=-x+a的大致图象,随着a的变化,要求f(x)的图象再y轴右侧的部分恒在g(x)的上方.可解得a的取值范围是[0,+∞]
和g(x)=-x+a的大致图象,随着a的变化,要求f(x)的图象再y轴右侧的部分恒在g(x)的上方.可解得a的取值范围是[0,+∞]
学生乙:在坐标平面内作出函数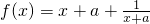 的大致图象,随着a的变化,要求f(x)的图象再y轴右侧的部分恒在直线y=2a的上方.可解得a的取值范围是[0,1].
的大致图象,随着a的变化,要求f(x)的图象再y轴右侧的部分恒在直线y=2a的上方.可解得a的取值范围是[0,1].
则以下对上述两位同学的解题方法和结论的判断都正确的是
- A.甲同学方法正确,结论错误
- B.乙同学方法正确,结论错误
- C.甲同学方法正确,结论正确
- D.乙同学方法错误,结论正确
已知数列 是各项均不为0的等差数列,公差为d,
是各项均不为0的等差数列,公差为d, 为其前n项和,且满足
为其前n项和,且满足 ,
, .数列
.数列 满足
满足 ,
, ,
, 为数列
为数列 的前n项和.
的前n项和.
(1)求数列 的通项公式
的通项公式 和数列
和数列 的前n项和
的前n项和 ;
;
(2)若对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)是否存在正整数
 ,使得
,使得 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【解析】第一问利用在 中,令n=1,n=2,
中,令n=1,n=2,
得 即
即
解得 ,,
,, [
[
又 时,
时, 满足
满足 ,
,
 ,
,

第二问,①当n为偶数时,要使不等式 恒成立,即需不等式
恒成立,即需不等式 恒成立.
恒成立.
 ,等号在n=2时取得.
,等号在n=2时取得.
 此时
此时 需满足
需满足 .
.
②当n为奇数时,要使不等式 恒成立,即需不等式
恒成立,即需不等式 恒成立.
恒成立.
 是随n的增大而增大, n=1时
是随n的增大而增大, n=1时 取得最小值-6.
取得最小值-6.
 此时
此时 需满足
需满足 .
.
第三问 ,
,
若 成等比数列,则
成等比数列,则 ,
,
即. 
由 ,可得
,可得 ,即
,即 ,
,
 .
. 
(1)(法一)在 中,令n=1,n=2,
中,令n=1,n=2,
得 即
即
解得 ,,
,, [
[
又 时,
时, 满足
满足 ,
,
 ,
,
 .
.
(2)①当n为偶数时,要使不等式 恒成立,即需不等式
恒成立,即需不等式 恒成立.
恒成立.
 ,等号在n=2时取得.
,等号在n=2时取得.
 此时
此时 需满足
需满足 .
.
②当n为奇数时,要使不等式 恒成立,即需不等式
恒成立,即需不等式 恒成立.
恒成立.
 是随n的增大而增大, n=1时
是随n的增大而增大, n=1时 取得最小值-6.
取得最小值-6.
 此时
此时 需满足
需满足 .
.
综合①、②可得 的取值范围是
的取值范围是 .
.
(3) ,
,
若 成等比数列,则
成等比数列,则 ,
,
即. 
由 ,可得
,可得 ,即
,即 ,
,
 .
. 
又 ,且m>1,所以m=2,此时n=12.
,且m>1,所以m=2,此时n=12.
因此,当且仅当m=2,
n=12时,数列 中的
中的 成等比数列
成等比数列
查看习题详情和答案>>