题目内容
现有问题:“对任意x>0,不等式x-a+ >0恒成立,求实数a的取值范围.”有两位同学用数形结合的方法分别提出了自己的解题思路和答案:
>0恒成立,求实数a的取值范围.”有两位同学用数形结合的方法分别提出了自己的解题思路和答案:学生甲:在一个坐标系内作出函数
 和g(x)=-x+a的大致图象,随着a的变化,要求f(x)的图象再y轴右侧的部分恒在g(x)的上方.可解得a的取值范围是[0,+∞]
和g(x)=-x+a的大致图象,随着a的变化,要求f(x)的图象再y轴右侧的部分恒在g(x)的上方.可解得a的取值范围是[0,+∞]学生乙:在坐标平面内作出函数
 的大致图象,随着a的变化,要求f(x)的图象再y轴右侧的部分恒在直线y=2a的上方.可解得a的取值范围是[0,1].
的大致图象,随着a的变化,要求f(x)的图象再y轴右侧的部分恒在直线y=2a的上方.可解得a的取值范围是[0,1].则以下对上述两位同学的解题方法和结论的判断都正确的是( )
A.甲同学方法正确,结论错误
B.乙同学方法正确,结论错误
C.甲同学方法正确,结论正确
D.乙同学方法错误,结论正确
【答案】分析:数形结合解决恒成立问题,应尽量使被研究函数是我们熟悉的基本函数,本例中学生甲使用的函数为一次函数和反比例函数与一次函数的简单复合,符合数形结合的要求,但学生甲的结论显然是错误的;对于学生乙,选择的函数是我们不太熟悉的函数,解决问题困难较大
解答:解:函数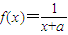 的图象是将函数y=
的图象是将函数y=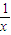 的图象向左(a>0),或向右(a<0)平移|a|个单位得到的
的图象向左(a>0),或向右(a<0)平移|a|个单位得到的
函数g(x)=-x+a的图象是斜率为-1,在y轴上的截距为a的直线,
当a=0和a=1时,两函数在y轴右侧的图象如图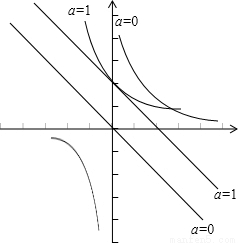
要使f(x)的图象再y轴右侧的部分恒在g(x)的上方
数形结合可知a的取值范围是[0,1].
故选A
点评:本题考查了数形结合解决不等式恒成立问题的方法,由于本题中两个函数都在动,给数形结合带来一定难度,解题时要善于从特殊值入手,理解题意,解决问题
解答:解:函数
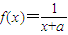 的图象是将函数y=
的图象是将函数y=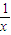 的图象向左(a>0),或向右(a<0)平移|a|个单位得到的
的图象向左(a>0),或向右(a<0)平移|a|个单位得到的函数g(x)=-x+a的图象是斜率为-1,在y轴上的截距为a的直线,
当a=0和a=1时,两函数在y轴右侧的图象如图

要使f(x)的图象再y轴右侧的部分恒在g(x)的上方
数形结合可知a的取值范围是[0,1].
故选A
点评:本题考查了数形结合解决不等式恒成立问题的方法,由于本题中两个函数都在动,给数形结合带来一定难度,解题时要善于从特殊值入手,理解题意,解决问题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
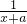 >0恒成立,求实数a的取值范围.”有两位同学用数形结合的方法分别提出了自己的解题思路和答案:
>0恒成立,求实数a的取值范围.”有两位同学用数形结合的方法分别提出了自己的解题思路和答案: 和g(x)=-x+a的大致图象,随着a的变化,要求f(x)的图象再y轴右侧的部分恒在g(x)的上方.可解得a的取值范围是[0,+∞]
和g(x)=-x+a的大致图象,随着a的变化,要求f(x)的图象再y轴右侧的部分恒在g(x)的上方.可解得a的取值范围是[0,+∞]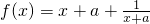 的大致图象,随着a的变化,要求f(x)的图象再y轴右侧的部分恒在直线y=2a的上方.可解得a的取值范围是[0,1].
的大致图象,随着a的变化,要求f(x)的图象再y轴右侧的部分恒在直线y=2a的上方.可解得a的取值范围是[0,1].