网址:http://m.1010jiajiao.com/timu_id_481897[举报]
一、 选择题(每小题5分,共60分)
BBDACA CDBDBA
二、填空题(每小题4分,共16分)
13. 14.
14. 15.
15. 16.
16.
三、解答题
17.(本小题满分12分)
解:(Ⅰ)∵ ,
,
由 ,得
,得
两边平方: =
= ,∴
,∴ =
= ………………6分
………………6分
(Ⅱ)∵ ,
,
∴ ,解得
,解得 ,
,
又∵ ,
∴
,
∴ ,
,
∴ ,
, ,
,
设 的夹角为
的夹角为 ,则
,则
 ,∴
,∴
即 的夹角为
的夹角为 . …………… 12分
. …………… 12分
18. (本小题满分12分)
解:(Ⅰ)小王在第三次考试中通过而领到驾照的概率为:
 ………………………6分
………………………6分
(Ⅱ)小王在一年内领到驾照的概率为:
 ………………12分
………………12分
19.(本小题满分12分)
(Ⅰ)证明:由已知得 ,所以
,所以 ,即
,即 ,
,
又 ,
, ,∴
,∴ ,
,
 平面
平面
∴平面 平面
平面 .……………………………4分(文6分)
.……………………………4分(文6分)
(Ⅱ)解:设 的中点为
的中点为 ,连接
,连接 ,则
,则 ∥
∥ ,
,
∴ 是异面直线
是异面直线 和
和 所成的角或其补角
所成的角或其补角
由(Ⅰ)知 ,在
,在 中,
中, ,
, ,
,
∴ .
.
所以异面直线 和
和 所成的角为
所成的角为 .…………………8分(文12分)
.…………………8分(文12分)
20.(本小题满分12分)
解:(Ⅰ)∵
据题意, ,
,
∴ ………………………4分
………………………4分
(Ⅱ)由(Ⅰ)知 ,
,
∴
则


















∴对于 ,
, 最小值为
最小值为 ………………… 8分
………………… 8分
∵ 的对称轴为
的对称轴为 ,且抛物线开口向下,
,且抛物线开口向下,
∴ 时,
时, 最小值为
最小值为 与
与 中较小的,
中较小的,
∵ ,
,
∴当 时,
时, 的最小值是-7.
的最小值是-7.
∴ 的最小值为-11. ………………………12分
的最小值为-11. ………………………12分
21.(本小题满分12分)
解:(Ⅰ)∵
∴
∴
令 ,则
,则 ,∴
,∴
 ,∴
,∴
∴ .……………6分
.……………6分
(Ⅱ)证明:由(Ⅰ)知:
记
用错位相减法求和得:
令 ,
,
∵
∴数列 是递减数列,∴
是递减数列,∴ ,
,
∴ .
.
即 .………………………12分
.………………………12分
(由 证明也给满分)
证明也给满分)
22.(本小题满分14分)
解:(Ⅰ)①当直线 轴时,
轴时,
则 ,此时
,此时 ,∴
,∴ .
.
(不讨论扣1分)
②当直线 不垂直于
不垂直于 轴时,
轴时, ,设双曲线的右准线为
,设双曲线的右准线为 ,
,
作 于
于 ,作
,作 于
于 ,作
,作 于
于 且交
且交 轴于
轴于
根据双曲线第二定义有: ,
,
而 到准线
到准线 的距离为
的距离为 .
.
由 ,得:
,得: ,
,
∴ ,∴
,∴ ,∵此时
,∵此时 ,∴
,∴
综上可知 .………………………………………7分
.………………………………………7分
(Ⅱ)设 :
: ,代入双曲线方程得
,代入双曲线方程得
∴
令 ,则
,则 ,且
,且 代入上面两式得:
代入上面两式得:
 ①
①
 ②
②
由①②消去 得
得
即 ③
③
由 有:
有: ,综合③式得
,综合③式得
由 得
得 ,解得
,解得
∴ 的取值范围为
的取值范围为 …………………………14分
…………………………14分
①当b=0,c>0时,方程f(x)=0只有一个实数根;
②当c=0时,y=f(x)是奇函数;
③y= f(x)的图象关于点(0,c)对称;
④函数f(x)至多有两个零点。
上述命题中的所有正确命题的序号是( )。
f(x)=x3,给出下列四个命题:
①f(x)是以4为周期的周期函数;
②f(x)在[1,3]上的解析式为f(x)=(2-x)3;
③f(x)图象的对称轴有x=±1;
④f(x)在点(
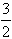 ,f(
,f(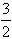 ))处的切线方程为3x+4y=5;
))处的切线方程为3x+4y=5;⑤函数f(x)在R上无最大值。
其中正确命题的序号是( )(写出所有正确命题的序号)。
设函数f(x)=x|x|+bx+c,给出下列四个命题:①当c=0时,f(x)是奇函数;②当b=0,c>0时,方程f(x)=0只有一个实根;③函数f(x)的图象关于点(0,c)对称;④方程f(x)=0至多有两个实根.其中正确命题的个数为
1
2
3
4