题目内容
设函数y=f(x)是定义域为R的奇函数,且满足f(x-2)= -f(x)对一切x∈R恒成立,当x∈[0,1]时,
f(x)=x3,给出下列四个命题:
①f(x)是以4为周期的周期函数;
②f(x)在[1,3]上的解析式为f(x)=(2-x)3;
③f(x)图象的对称轴有x=±1;
④f(x)在点(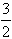 ,f(
,f(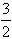 ))处的切线方程为3x+4y=5;
))处的切线方程为3x+4y=5;
⑤函数f(x)在R上无最大值。
其中正确命题的序号是( )(写出所有正确命题的序号)。
f(x)=x3,给出下列四个命题:
①f(x)是以4为周期的周期函数;
②f(x)在[1,3]上的解析式为f(x)=(2-x)3;
③f(x)图象的对称轴有x=±1;
④f(x)在点(
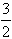 ,f(
,f(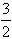 ))处的切线方程为3x+4y=5;
))处的切线方程为3x+4y=5;⑤函数f(x)在R上无最大值。
其中正确命题的序号是( )(写出所有正确命题的序号)。
①②③④

练习册系列答案
相关题目