题目内容
(B题)设函数f(x)=|x|x+bx+c,给出下列四个命题:
①当b=0,c>0时方程f(x)=0有且只有一个实数根;
②当c=0时,y=f(x)是奇函数;
③?x∈R有f(-x)=2c-f(x);
④方程f(x)=0至多有两个实数根.
则上述命题中,所有正确命题的序号为
①当b=0,c>0时方程f(x)=0有且只有一个实数根;
②当c=0时,y=f(x)是奇函数;
③?x∈R有f(-x)=2c-f(x);
④方程f(x)=0至多有两个实数根.
则上述命题中,所有正确命题的序号为
①②③
①②③
.分析:分别根据条件,讨论b,c的取值进行判断.
①当b=0时,得f(x)=x|x|+c在R上为单调增函数,方程f(x)=0只有一个实根.
②利用函数奇偶性的定义可判断.③利用函数图象关于点对称的定义,可证得函数f(x)图象关于点(0,c)对称.
④举出反例如c=0,b=-2,可以判断.
①当b=0时,得f(x)=x|x|+c在R上为单调增函数,方程f(x)=0只有一个实根.
②利用函数奇偶性的定义可判断.③利用函数图象关于点对称的定义,可证得函数f(x)图象关于点(0,c)对称.
④举出反例如c=0,b=-2,可以判断.
解答:解:①b=0,c>0时,得f(x)=x|x|+c=
,在R上为单调增函数,且值域为R,故方程f(x)=0,只有一个实数根,故①正确.
②当c=0时,函数f(x)=x|x|+bx为奇函数,故②正确.
③∵f(-x)=-x|x|-bx+c,∴f(-x)+f(x)=2c,可得函数f(x)的图象关于点(0,c)对称,故③正确.
④当c=0,b=-2,f(x)=x|x|-2x=0的根有x=0,x=2,x=-2故④错误.
故答案为:①②③.
|
②当c=0时,函数f(x)=x|x|+bx为奇函数,故②正确.
③∵f(-x)=-x|x|-bx+c,∴f(-x)+f(x)=2c,可得函数f(x)的图象关于点(0,c)对称,故③正确.
④当c=0,b=-2,f(x)=x|x|-2x=0的根有x=0,x=2,x=-2故④错误.
故答案为:①②③.
点评:本题考查了函数奇偶性、对称性、单调性以及二次函数的图象和性质.对函数奇偶性和单调性的充分理解,并用于二次函数当中,是解决本题的关键.

练习册系列答案
相关题目
 短长度为
短长度为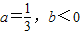 ,y=f(x)在x=0处取得极值-1,且过点(0,0)可作曲线y=f(x)的三条切线,求b的取值范围.
,y=f(x)在x=0处取得极值-1,且过点(0,0)可作曲线y=f(x)的三条切线,求b的取值范围.