网址:http://m.1010jiajiao.com/timu_id_478869[举报]
一、选择题 ACCBC BBCCD
二、填空题: ,
, ,
, ,
, ,
, ,
, ,①②④
,①②④
18(Ⅰ)由题意“ 且
且 ”表示“答完
”表示“答完 题,第一题答对,第二题答错;或第一题答对,第二题也答对” 此时概率
题,第一题答对,第二题答错;或第一题答对,第二题也答对” 此时概率
 …6分
…6分
(Ⅱ)P( )=
)= =
= , P(
, P( )=
)= =
= ,………9分
,………9分

-3
-1
1
3





P( )=
)= =
= ,
P(
,
P( )=
)= =
=
∴ 的分布列为
的分布列为
12分
∴ ……14分
……14分
19解:(Ⅰ) 连接 交
交 于点
于点 ,连接
,连接 .
.
在 中,
中,
 分别为
分别为 中点,
中点,
 .
.

 平面
平面 ,
, 平面
平面 ,
,
 平面
平面 . …………(6分)
. …………(6分)
(Ⅱ) 法一:过 作
作 于
于 ,由三垂线定理得
,由三垂线定理得 ,
,
故∠ 为二面角
为二面角 的平面角. ……………………………………(9分)
的平面角. ……………………………………(9分)
令 ,则
,则 ,又
,又 ,
,
在 △
△ 中,
中, ,
,
解得 。
。

 当
当 时,二面角
时,二面角 的正弦值为
的正弦值为 . ………………(14分)
. ………………(14分)
法二:设 ,取
,取 中点
中点 ,连接
,连接 ,
,
以 为坐标原点建立空间直角坐标系,如右图所示:
为坐标原点建立空间直角坐标系,如右图所示:
则 ,
,
则 .
.
设平面 的法向量为
的法向量为 ,平面
,平面 的法向量为
的法向量为 ,
,
则有 ,
, ,即
,即 ,
, ,
,
设 ,则
,则 ,
,



 ,解得
,解得 .
.
 即当
即当 时,二面角
时,二面角 的正弦值为
的正弦值为 . …………………(14分)
. …………………(14分)
20.(1)  ;
;
(2)轨迹方程为 (
( )
)
(1)当 时,轨迹方程为
时,轨迹方程为 (
( ),表示抛物线弧段。
),表示抛物线弧段。
(2)当 时,轨迹方程为
时,轨迹方程为 ,
,
A)当 表示椭圆弧段; B)当
表示椭圆弧段; B)当 时表示双曲线弧段。
时表示双曲线弧段。
21.
Ⅰ) …………(2分)
…………(2分)
令 ,则
,则
当 时,
时, ;当
;当 时
时 
故有极大值 …………(4分)
…………(4分)
Ⅱ)∵ =a+
=a+ ,x∈(0,e),
,x∈(0,e), ∈[
∈[ ,+∞
,+∞
(1)若a≥- ,则
,则 ≥0,从而f(x)在(0,e)上增函数.
≥0,从而f(x)在(0,e)上增函数.
∴f(x)max =f(e)=ae+1≥0.不合题意. …………………………………7分
(2)若a<- ,
,  >
> a+
a+ >0,即0<x<-
>0,即0<x<-
由
 a+
a+ <0,即-
<0,即- <x≤e.
<x≤e.
∴f(x) =f(-
=f(- )=-1+ln(-
)=-1+ln(- ).
).
令-1+ln(- )=-3,则ln(-
)=-3,则ln(- )=-2.∴-
)=-2.∴- =e
=e ,
,
即a=-e2. ∵-e2<- ,∴a=-e2为所求. ……………………………10分
,∴a=-e2为所求. ……………………………10分
Ⅲ)由Ⅰ)结论, =f(1)=-1.∴f(x)=-x+lnx≤-1,从而lnx≤x-1.
=f(1)=-1.∴f(x)=-x+lnx≤-1,从而lnx≤x-1.
令g(x)=|f(x)|- -
- =x-lnx-
=x-lnx- -
- =x-(1+
=x-(1+ )lnx-
)lnx- ……12分
……12分
(1)当0<x<2时,有g(x)≥x-(1+ )(x-1)-
)(x-1)- =
= -
- >0.
>0.
(2)当x≥2时,g′(x)=1-[(- )lnx+(1+
)lnx+(1+ )?
)? ]=
]=
= .
.
∴g(x)在[2,+∞ 上增函数,∴g(x)≥g(2)=
上增函数,∴g(x)≥g(2)=
综合(1)、(2)知,当x>0时,g(x)>0,即|f(x)|> .
.
故原方程没有实解. ………………………………16分
22.证明:(I)
①当 , …………2分
, …………2分
②假设 ,
,
则 时不等式也成立,
时不等式也成立, …………4分
…………4分
(II)由 ,
,
由
…………5分

又 …………7分
…………7分
 …………8分
…………8分
(III) ,
,
 , …………10分
, …………10分

 的等比数列,…………12分
的等比数列,…………12分

 …………14分
…………14分
(1)在等差数列{an}中,已知S10=30,S20=100,求S30.
(2)在等差数列{an}中,根据要求完成下列表格,并对①、②式加以证明(其中m、m1、m2、n∈N*).
| 用Sm表示S2m | S2m=2Sm+m2d |
用 、 、 表示 表示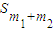 |  =______① =______① |
| 用Sm表示Snm | Snm=______② |
(ⅰ) 类比(2)中①式,在等比数列{bn}中,写出相应的结论.
(ⅱ) (解答本题,最多得5分)类比(2)中②式,在等比数列{bn}中,写出相应的结论.
(ⅲ) (解答本题,最多得6分)在等差数列{an}中,将(2)中的①推广到一般情况.
(ⅳ) (解答本题,最多得6分)在等比数列{bn}中,将(2)中的①推广到一般情况.
查看习题详情和答案>>
(1)在等差数列{an}中,已知S10=30,S20=100,求S30.
(2)在等差数列{an}中,根据要求完成下列表格,并对①、②式加以证明(其中m、m1、m2、n∈N*).
| 用Sm表示S2m | S2m=2Sm+m2d | ||||
| 用Sm1、Sm2表示Sm1+m2 | Sm1+m2= Sm1+Sm2+m1m2d Sm1+Sm2+m1m2d ① | ||||
| 用Sm表示Snm | Snm= nSm+
nSm+ ②
|
(ⅰ) 类比(2)中①式,在等比数列{bn}中,写出相应的结论.
(ⅱ) (解答本题,最多得5分)类比(2)中②式,在等比数列{bn}中,写出相应的结论.
(ⅲ) (解答本题,最多得6分)在等差数列{an}中,将(2)中的①推广到一般情况.
(ⅳ) (解答本题,最多得6分)在等比数列{bn}中,将(2)中的①推广到一般情况.
(1)空间直角坐标系O-XYZ中,点A(-2,3,-1)关于平面XOZ的对称点为A′(-2,-3,-1).
(2)棱长为1的正方体外接球表面积为8π.
(3)已知等比数列{an}的前n项和为Sn,若Sn=2n+c(c为常数),则c=-1.
(4)若非零实数a1,b1,a2,b2满足
| a1 |
| a2 |
| b1 |
| b2 |
(5)已知等差数列{an}的前n项和为Sn,则点P1(1,
| S1 |
| 1 |
| S2 |
| 2 |
| Sn |
| n |
以上正确的命题是