摘要：(3) 2R= ------12分
网址：http://m.1010jiajiao.com/timu_id_476248[举报]
已知正项数列
的前n项和
满足：
，
（1）求数列的通项
和前n项和；
（2）求数列
的前n项和
；
（3）证明：不等式 
对任意的
，
都成立．
【解析】第一问中，由于所以
两式作差
，然后得到
从而
得到结论
第二问中，
利用裂项求和的思想得到结论。
第三问中，
又
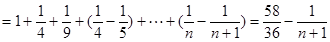
结合放缩法得到。
解：（1）∵ ∴
∴
∴
∴ ………2分
又∵正项数列，∴
∴
又n=1时，
∴
∴数列是以1为首项，2为公差的等差数列……………3分
∴
…………………4分
∴
…………………5分
（2）
…………………6分
∴
…………………9分
（3）
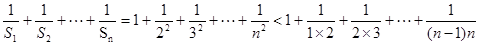
…………………12分
又
，
∴不等式 对任意的，都成立．
查看习题详情和答案>>
（2012•宝鸡模拟）某休闲会馆拟举行“五一”庆祝活动，每位来宾交30元的入场费，可参加一次抽奖活动．抽奖活动规则是：从一个装有分值分别为1，2，3，4，5，6的六个相同小球的抽奖箱中，有放回的抽取两次，每次抽取一个球，规定：若抽得两球的分值之和为12分，则获得价值为m元的礼品；若抽得两球的分值之和为11分或10分，则获得价值为100元的礼品；若抽得两球的分值之和低于10分，则不获奖．
（1）求每位会员获奖的概率；
（2）假设这次活动会馆既不赔钱也不赚钱，则m应为多少元？
查看习题详情和答案>>
（1）求每位会员获奖的概率；
（2）假设这次活动会馆既不赔钱也不赚钱，则m应为多少元？
北京时间2011年3月11日13时46分，在日本东海岸附近海域发生里氏9级地震后引发海啸，导致福岛第一核电站受损严重．3月12日以来，福岛第一核电站的4台机组（编号分别为1、2、3、4）的核反应堆相继发生爆炸，放射性物质泄漏到外部．某评估机构预估日本在十年内修复该核电站第1、2、3、4号机组的概率分别为
，
，
，
．假设这4台机组能否被修复相互独立．
（1）求十年内这4台机组中恰有1台机组被修复的概率；
（2）求十年内这4台机组中被修复的机组的总数为随机变量ξ，求随机变量ξ的分布列和数学期望Eξ．
查看习题详情和答案>>
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
（1）求十年内这4台机组中恰有1台机组被修复的概率；
（2）求十年内这4台机组中被修复的机组的总数为随机变量ξ，求随机变量ξ的分布列和数学期望Eξ．
已知函数f（x）=sin（ωx+φ），（ω＞0，，0＜φ＜π）的一系列对应值如表：
（Ⅰ）求f（x）的解析式；
（Ⅱ）在△ABC中，a、b、c分别是△ABC的对边，若f(A)=
，c=2，a=
b，求△ABC的面积．
查看习题详情和答案>>
| x | -
|
|
|
|
| ||||||||||
| y | 0 | 1 | 0 | -1 | 0 |
（Ⅱ）在△ABC中，a、b、c分别是△ABC的对边，若f(A)=
| 1 |
| 2 |
| 3 |