题目内容
12分)设函数f(x)=2x3-3(a+1)x2+6ax+8,a∈R,
(1)若f(x)在x=3处取得极值,求实数a的值;
(2)在(1)的条件下,求函数f(x)的单调区间.
(1)若f(x)在x=3处取得极值,求实数a的值;
(2)在(1)的条件下,求函数f(x)的单调区间.
分析:(1)先求原函数的导数;再根据f(x)在x=3处取得极值对应的结论f′(3)=0即可求实数a的值;
(2)先求原函数的导数,根据f′(x)>0求得的区间是单调增区间,f′(x)<0求得的区间是单调减区间,即可.
(2)先求原函数的导数,根据f′(x)>0求得的区间是单调增区间,f′(x)<0求得的区间是单调减区间,即可.
解答:解:因为f(x)=2x3-3(a+1)x2+6ax+8,
所以:f′(x)=6x2-6(a+1)x+6a=6(x-a)(x-1)
(1)∵f(x)在x=3处取得极值
∴f′(3)=0⇒6(3-a)(3-1)=0⇒a=3;
(2)∵a=3,
∴f′(x)=6(x-3)(x-1).
令f′(x)>0⇒x>3或x<1.
令f′(x)<0⇒1<x<3
所以函数的增区间为(-∞,1],[3,+∞).
减区间为:[1,3].
所以:f′(x)=6x2-6(a+1)x+6a=6(x-a)(x-1)
(1)∵f(x)在x=3处取得极值
∴f′(3)=0⇒6(3-a)(3-1)=0⇒a=3;
(2)∵a=3,
∴f′(x)=6(x-3)(x-1).
令f′(x)>0⇒x>3或x<1.
令f′(x)<0⇒1<x<3
所以函数的增区间为(-∞,1],[3,+∞).
减区间为:[1,3].
点评:本小题主要考查函数单调性的应用、利用导数研究函数的单调性、不等式的解法等基础知识,考查运算求解能力,转化思想.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 ,求a的取值范围。
,求a的取值范围。 ,求a的取值范围。
,求a的取值范围。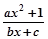 是奇函数(a,b,c都是整数)且f(1)=2,f(2)<3
是奇函数(a,b,c都是整数)且f(1)=2,f(2)<3 +
+ -1.
-1. <
< <1+
<1+ 成立.
成立.