摘要:=, 所以S=3012
网址:http://m.1010jiajiao.com/timu_id_475751[举报]
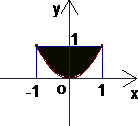 利用计算机随机模拟方法计算图中阴影面积(如图所示)
利用计算机随机模拟方法计算图中阴影面积(如图所示)第一步:利用计算机产生两个0~1区间的均匀随机数,x,y,其中-1<x<1,0<y<1;
第二步:拟(x,y)为点的坐标.共做此实验N次.若落在阴影部分的点的个数为N1,
则可以计算阴影部分的面积S.例如:做了2000次实验,即N=2000,模拟得到N1=1396,所以S=
1.396
1.396
.
利用计算机随机模拟方法计算图中阴影面积(如图所示)
第一步:利用计算机产生两个0~1区间的均匀随机数,x,y,其中-1<x<1,0<y<1;
第二步:拟(x,y)为点的坐标.共做此实验N次.若落在阴影部分的点的个数为N1,
则可以计算阴影部分的面积S.例如:做了2000次实验,即N=2000,模拟得到N1=1396,所以S= .
 查看习题详情和答案>>
查看习题详情和答案>>
第一步:利用计算机产生两个0~1区间的均匀随机数,x,y,其中-1<x<1,0<y<1;
第二步:拟(x,y)为点的坐标.共做此实验N次.若落在阴影部分的点的个数为N1,
则可以计算阴影部分的面积S.例如:做了2000次实验,即N=2000,模拟得到N1=1396,所以S= .
 查看习题详情和答案>>
查看习题详情和答案>>
 利用计算机随机模拟方法计算图中阴影面积(如图所示)
利用计算机随机模拟方法计算图中阴影面积(如图所示)
第一步:利用计算机产生两个0~1区间的均匀随机数,x,y,其中-1<x<1,0<y<1;
第二步:拟(x,y)为点的坐标.共做此实验N次.若落在阴影部分的点的个数为N1,
则可以计算阴影部分的面积S.例如:做了2000次实验,即N=2000,模拟得到N1=1396,所以S=________.
查看习题详情和答案>>
(2005•上海模拟)(1)若直角三角形两直角边长之和为12,求其周长p的最小值;
(2)若三角形有一个内角为arccos
,周长为定值p,求面积S的最大值;
(3)为了研究边长a、b、c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值,现有解法如下:S=
absinC≤
×9×8sinC=36sinC,要使S的值最大,则应使sinC最大,即使∠C最大,也就是使∠C所对的边c边长最大,所以,当a?9,b?8,c?4时该三角形面积最大,此时cosC=
,sinC=
,所以,该三角形面积的最大值是
.以上解答是否正确?若不正确,请你给出正确的解答.
查看习题详情和答案>>
(2)若三角形有一个内角为arccos
| 7 |
| 9 |
(3)为了研究边长a、b、c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值,现有解法如下:S=
| 1 |
| 2 |
| 1 |
| 2 |
| 43 |
| 48 |
| ||
| 48 |
3
| ||
| 4 |
某校要从甲、乙两名优秀短跑选手中选一名选手参加全市中学生田径百米比赛,该校预先对这两名选手测试了8次,测试成绩如下:
根据测试成绩,派
查看习题详情和答案>>
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 | 第8次 | |
| 甲成绩(秒) | 12.1 | 12.2 | 13 | 12.5 | 13.1 | 12.5 | 12.4 | 12.2 |
| 乙成绩(秒) | 12 | 12.4 | 12.8 | 13 | 12.2 | 12.8 | 12.3 | 12.5 |
乙选手参赛更好.
乙选手参赛更好.
(填甲或乙)选手参赛更好,理由是因为
=
=12.5,S甲2=0.12,S乙2=0.10,所以乙选手成绩比甲选手成绩稳定,派乙选手参赛更好.
. |
| x甲 |
. |
| x乙 |
因为
=
=12.5,S甲2=0.12,S乙2=0.10,所以乙选手成绩比甲选手成绩稳定,派乙选手参赛更好.
.. |
| x甲 |
. |
| x乙 |