解:(1)判断:AB//平面DEF------------------..2分——青夏教育精英家教网——

摘要：解:(1)判断:AB//平面DEF------------------..2分

网址：http://m.1010jiajiao.com/timu_id_475570[举报]

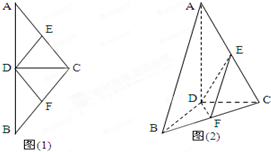（2012•韶关二模）如图（1）在等腰△ABC中，D、E、F分别是AB、AC、BC边的中点，现将△ACD沿CD翻折，使得平面ACD⊥平面BCD．（如图（2））
（1）求证：AB∥平面DEF；
（2）求证：BD⊥AC；
（3）设三棱锥A-BCD的体积为V₁、多面体ABFED的体积为V₂，求V₁：V₂的值．

查看习题详情和答案>>

如图（1）在等腰△ABC中，D、E、F分别是AB、AC、BC边的中点，现将△ACD沿CD翻折，使得平面ACD⊥平面BCD．（如图（2））
（1）求证：AB∥平面DEF；
（2）求证：BD⊥AC；
（3）设三棱锥A-BCD的体积为V₁、多面体ABFED的体积为V₂，求V₁：V₂的值．

查看习题详情和答案>>

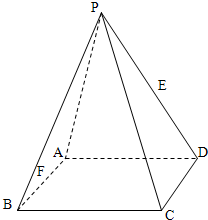如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD，
AB=

AD，E是线段PD上的点，F是线段AB上的点，且

=λ(λ＞0)
（1）判断EF与平面PBC的关系，并证明；
（2）当λ为何值时，DF⊥平面PAC？并证明．查看习题详情和答案>>

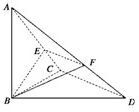如图，在△BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，∠ADB=60°，E、F分别是AC、AD上的动点，且

=λ（0＜λ＜1）．
（1）判断EF与平面ABC的位置关系并给予证明；
（2）是否存在λ，使得平面BEF⊥平面ACD，如果存在，求出λ的值，如果不存在，说明理由．

查看习题详情和答案>>

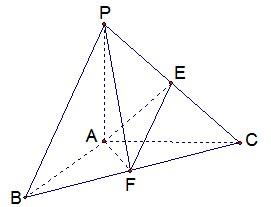三棱锥P-ABC中，PA=AB=AC，∠BAC=120°，PA⊥平面ABC，点E、F分别为线段PC、BC的中点，
（1）判断PB与平面AEF的位置关系并说明理由；
（2）求直线PF与平面PAC所成角的正弦值．查看习题详情和答案>>