题目内容
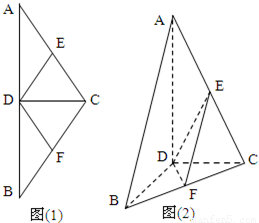
如图(1)在等腰△ABC中,D、E、F分别是AB、AC、BC边的中点,现将△ACD沿CD翻折,使得平面ACD⊥平面BCD.(如图(2))(1)求证:AB∥平面DEF;
(2)求证:BD⊥AC;
(3)设三棱锥A-BCD的体积为V1、多面体ABFED的体积为V2,求V1:V2的值.

【答案】分析:(1)先利用三角形中位线定理证明EF∥AB,再利用线面平行的判定定理证明AB∥平面DEF即可;
(2)先利用面面垂直的性质定理证明BD⊥平面ACD,再利用线面垂直的定义证明BD⊥AC即可;
(3)先利用面面垂直的性质定理证明AD⊥平面BCD,从而得三棱锥A-BCD的体积为V1、再利用线面垂直的性质求三棱锥E-CDF的体积为 ,从而得多面体的体积为
,从而得多面体的体积为 ,从而确定所求体积之比
,从而确定所求体积之比
解答: 解:(1)证明:如图:在△ABC中,由E、F分别是AC、BC中点,得EF∥AB,
解:(1)证明:如图:在△ABC中,由E、F分别是AC、BC中点,得EF∥AB,
又AB?平面DEF,EF?平面DEF,
∴AB∥平面DEF.
(2)∵平面ACD⊥平面BCD于CD
BD⊥CD,且BD?平面BCD
∴BD⊥平面ACD,又AC?平面ACD
∴BD⊥AC.
(3))∵平面ACD⊥平面BCD于CD
AD⊥CD,且AD?平面ACD
∴AD⊥平面BCD
∴AD是三棱锥A-BCD的高
∴
又∵E、F分别是AC、BC边的中点,
∴三棱锥E-CDF的高是三棱锥A-BCD高的一半,即
三棱锥E-CDF的底面积是三棱锥A-BCD底面积的一半,即 S△BCD
S△BCD
∴三棱锥E-CDF的体积
∴
∴V1:V2=4:3.
点评:本题主要考查了线面平行的判定定理,面面垂直的性质定理,线面垂直的定义和性质,三棱锥体积的计算公式,辨清几何体中的垂直关系是解决本题的关键
(2)先利用面面垂直的性质定理证明BD⊥平面ACD,再利用线面垂直的定义证明BD⊥AC即可;
(3)先利用面面垂直的性质定理证明AD⊥平面BCD,从而得三棱锥A-BCD的体积为V1、再利用线面垂直的性质求三棱锥E-CDF的体积为
 ,从而得多面体的体积为
,从而得多面体的体积为 ,从而确定所求体积之比
,从而确定所求体积之比解答:
 解:(1)证明:如图:在△ABC中,由E、F分别是AC、BC中点,得EF∥AB,
解:(1)证明:如图:在△ABC中,由E、F分别是AC、BC中点,得EF∥AB,又AB?平面DEF,EF?平面DEF,
∴AB∥平面DEF.
(2)∵平面ACD⊥平面BCD于CD
BD⊥CD,且BD?平面BCD
∴BD⊥平面ACD,又AC?平面ACD
∴BD⊥AC.
(3))∵平面ACD⊥平面BCD于CD
AD⊥CD,且AD?平面ACD
∴AD⊥平面BCD
∴AD是三棱锥A-BCD的高
∴

又∵E、F分别是AC、BC边的中点,
∴三棱锥E-CDF的高是三棱锥A-BCD高的一半,即

三棱锥E-CDF的底面积是三棱锥A-BCD底面积的一半,即
 S△BCD
S△BCD∴三棱锥E-CDF的体积

∴

∴V1:V2=4:3.
点评:本题主要考查了线面平行的判定定理,面面垂直的性质定理,线面垂直的定义和性质,三棱锥体积的计算公式,辨清几何体中的垂直关系是解决本题的关键

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
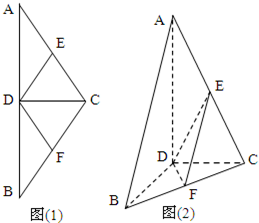 (2012•北海一模)如图(1)在等腰△ABC中,D,E,F分别是AB,AC和BC边的中点,∠ACB=120°,现将△ABC沿CD翻折成直二面角A-DC-B.(如图(2))
(2012•北海一模)如图(1)在等腰△ABC中,D,E,F分别是AB,AC和BC边的中点,∠ACB=120°,现将△ABC沿CD翻折成直二面角A-DC-B.(如图(2))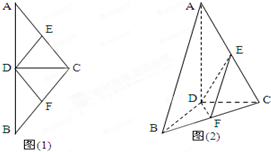 (2012•韶关二模)如图(1)在等腰△ABC中,D、E、F分别是AB、AC、BC边的中点,现将△ACD沿CD翻折,使得平面ACD⊥平面BCD.(如图(2))
(2012•韶关二模)如图(1)在等腰△ABC中,D、E、F分别是AB、AC、BC边的中点,现将△ACD沿CD翻折,使得平面ACD⊥平面BCD.(如图(2))