网址：http://m.1010jiajiao.com/timu_id_475522[举报]
假设一个人从出生到死亡，在每个生日都测量身高，并作出这些数据散点图，则这些点将不会落在一条直线上，但在一段时间内的增长数据有时可以用线性回归来分析．下表是一位母亲给儿子作的成长记录：
| 年龄／周岁 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 身高／cm | 90.8 | 97.6 | 104.2 | 110.9 | 115.6 | 122.0 | 128.5 |
| 年龄／周岁 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 身高／cm | 134.2 | 140.8 | 147.6 | 154.2 | 160.9 | 167.6 | 173.0 |
（1）作出这些数据的散点图；
（2）求出这些数据的回归方程；
（3）对于这个例子，你如何解释回归系数的含义？
（4）用下一年的身高减去当年的身高，计算他每年身高的增长数，并计算他从3~16岁身高的年均增长数．
（5）解释一下回归系数与每年平均增长的身高之间的联系．
查看习题详情和答案>>想象一下一个人从出生到死亡，在每个生日都测量身高，并作出这些数据散点图，这些点将不会落在一条直线上．但在一段时间内的增长数据有时可以用线性回归来分析．下表是一位母亲给儿子作的成长记录：
|
年龄 /周岁 |
3 |
4 |
5 |
6 |
|
身高 /cm |
90.8 |
97.6 |
104.2 |
110.9 |
|
年龄 /周岁 |
7 |
8 |
9 |
10 |
|
身高 /cm |
115.6 |
122.0 |
128.5 |
134.2 |
|
年龄 /周岁 |
11 |
12 |
13 |
14 |
|
身高 /cm |
140.8 |
147.6 |
154.2 |
160.9 |
|
年龄 /周岁 |
15 |
16 |
||
|
身高 /cm |
167.6 |
173.0 |
(1)作出这些数据的散点图.
(2)求出这些数据的回归方程.
(3)对于这个例子，你如何解释斜率的含义？
(4)用下一年的身高减去当年的身高，计算每年身高的增长数，并计算从3到16岁身高的平均增长数.
(5)解释一下斜率与每年平均增长的身高之间的联系.
查看习题详情和答案>>| π |
| 2 |
| x |
|
|
|
|
| ||||||||||||||||
| ωx+φ | 0 |
|
π |
|
2π | ||||||||||||||||
| Asin（ωx+φ） | 0 | 2 | 0 | -2 |
（2）当x∈[
| π |
| 3 |
| 5π |
| 12 |
（本小题满分12分）已知f (x)＝(1＋x)m＋(1＋2x)n(m，n∈N*)的展开式中x的系数为11.
(1)求x2的系数的最小值；
(2)当x2的系数取得最小值时，求f (x)展开式中x的奇次幂项的系数之和．
解： (1)由已知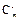
＋2
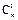＝11，∴m＋2n＝11，x2的系数为
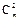＋22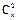
＝
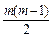＋2n(n－1)＝
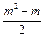＋(11－m)(
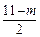－1)＝(m－
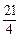)2＋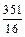
.
∵m∈N*，∴m＝5时，x2的系数取最小值22，此时n＝3.
(2)由(1)知，当x2的系数取得最小值时，m＝5，n＝3，
∴f (x)＝(1＋x)5＋(1＋2x)3.设这时f (x)的展开式为f (x)＝a0＋a1x＋a2x2＋…＋a5x5，
令x＝1，a0＋a1＋a2＋a3＋a4＋a5＝25＋
33，
令x＝－1，a0－a1＋a2－a3＋a4－a5＝－1，
两式相减得2(a1＋a3＋a5)＝60， 故展开式中x的奇次幂项的系数之和为30.
(1)求x2的系数的最小值；
(2)当x2的系数取得最小值时，求f (x)展开式中x的奇次幂项的系数之和．
解： (1)由已知
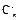＋2
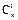＝11，∴m＋2n＝11，x2的系数为
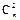＋22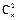
＝
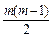＋2n(n－1)＝
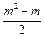＋(11－m)(
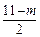－1)＝(m－
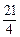)2＋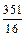
.∵m∈N*，∴m＝5时，x2的系数取最小值22，此时n＝3.
(2)由(1)知，当x2的系数取得最小值时，m＝5，n＝3，
∴f (x)＝(1＋x)5＋(1＋2x)3.设这时f (x)的展开式为f (x)＝a0＋a1x＋a2x2＋…＋a5x5，
令x＝1，a0＋a1＋a2＋a3＋a4＋a5＝25＋
33，令x＝－1，a0－a1＋a2－a3＋a4－a5＝－1，
两式相减得2(a1＋a3＋a5)＝60， 故展开式中x的奇次幂项的系数之和为30.