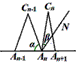摘要:(1) 由表1可知.当时.,那么.当时.y= ,(2)该公司职工小陈和大李2007年治病花费的医疗费和他们个人实际承担的费用如表2:职工治病花费的医疗费x(元)个人实际承担的费用y(元)小陈300280大李500320
网址:http://m.1010jiajiao.com/timu_id_474454[举报]
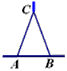
小知识:如图,我们称两臂长度相等(即CA=CB)的圆规为等臂圆规,当等臂圆规的两脚摆放在一条直线上时,若张角∠ACB=x°,则底角∠CAB=∠CBA=(90-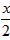 )°,
)°,
请运用上述知识解决问题:
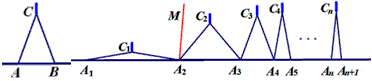
如图,n个相同规格的等臂圆规的两脚依次摆放在同一条直线上,其张角度数变化如下:
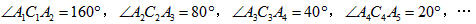
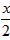 )°,
)°,请运用上述知识解决问题:
如图,n个相同规格的等臂圆规的两脚依次摆放在同一条直线上,其张角度数变化如下:
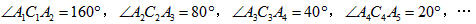
(1)①由题意可得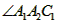 =____°;
=____°;
②若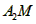 平
平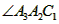 ,则
,则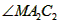 =____°;
=____°;
(2)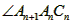 =____°(用含n的代数式表示);
=____°(用含n的代数式表示);
(3)当n≥3时,设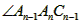 的度数为a,
的度数为a,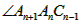 的角平分线
的角平分线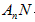 与
与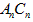 构成的角的度数为β,那么α与β之间的等量关系是____,请说明理由。(提示:可以借助上面的局部示意图)
构成的角的度数为β,那么α与β之间的等量关系是____,请说明理由。(提示:可以借助上面的局部示意图)
查看习题详情和答案>>
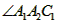 =____°;
=____°;②若
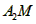 平
平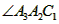 ,则
,则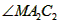 =____°;
=____°;(2)
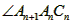 =____°(用含n的代数式表示);
=____°(用含n的代数式表示);(3)当n≥3时,设
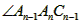 的度数为a,
的度数为a,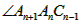 的角平分线
的角平分线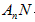 与
与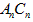 构成的角的度数为β,那么α与β之间的等量关系是____,请说明理由。(提示:可以借助上面的局部示意图)
构成的角的度数为β,那么α与β之间的等量关系是____,请说明理由。(提示:可以借助上面的局部示意图) 小知识:如图,我们称两臂长度相等(即![]() )的圆规为等臂圆规. 当等臂圆规的两脚摆放在一条直线上时,若张角
)的圆规为等臂圆规. 当等臂圆规的两脚摆放在一条直线上时,若张角![]() ,则底角
,则底角![]()

请运用上述知识解决问题:
如图,![]() 个相同规格的等臂圆规的两脚依次摆放在同一条直线上,其张角度数变化如下:
个相同规格的等臂圆规的两脚依次摆放在同一条直线上,其张角度数变化如下:
![]() ,
,![]() ,
, ![]() ,
,![]() ,…
,…
(1)①由题意可得![]() = º;
= º;
②若![]() 平分
平分![]() ,则
,则![]() = º;
= º;
(2)![]() = º(用含
= º(用含![]() 的代数式表示);
的代数式表示);
(3)当![]() 时,设
时,设![]() 的度数为
的度数为![]() ,
,![]() 的角平分线
的角平分线![]() 与
与![]() 构成的角的度数为
构成的角的度数为![]() ,那么
,那么![]() 与
与![]() 之间的等量关系是 ,请说明理由. (提示:可以借助下面的局部示意图)
之间的等量关系是 ,请说明理由. (提示:可以借助下面的局部示意图)

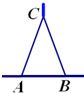 小知识:如图,我们称两臂长度相等(即CA=CB)的圆规为等臂圆规.当等臂圆规的两脚摆放在一条直线上时,若张角∠ACB=x°,则底角∠CAB=∠CBA=(90-
小知识:如图,我们称两臂长度相等(即CA=CB)的圆规为等臂圆规.当等臂圆规的两脚摆放在一条直线上时,若张角∠ACB=x°,则底角∠CAB=∠CBA=(90-| x | 2 |
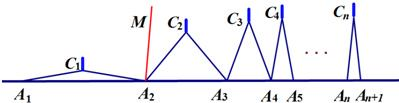
请运用上述知识解决问题:如图,n个相同规格的等臂圆规的两脚依次摆放在同一条直线上,其张角度数变化如下:∠A1C1A2=160°,∠A2C2A3=80°,∠A3C3A4=40°,∠A4C4A5=20°,…
(1)①由题意可得∠A1A2C1=
②若A2M平分∠A3A2C1,则∠MA2C2=
(2)∠An+1AnCn=
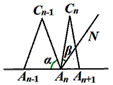
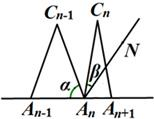
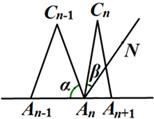
(3)当n≥3时,设∠An-1AnCn-1的度数为a,∠An+1AnCn-1的角平分线AnN与AnCn构成的角的度数为β,那么a与β之间的等量关系是
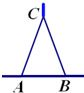 小知识:如图,我们称两臂长度相等(即CA=CB)的圆规为等臂圆规.当等臂圆规的两脚摆放在一条直线上时,若张角∠ACB=x°,则底角∠CAB=∠CBA=(90-
小知识:如图,我们称两臂长度相等(即CA=CB)的圆规为等臂圆规.当等臂圆规的两脚摆放在一条直线上时,若张角∠ACB=x°,则底角∠CAB=∠CBA=(90- )°.
)°.
请运用上述知识解决问题:如图,n个相同规格的等臂圆规的两脚依次摆放在同一条直线上,其张角度数变化如下:∠A1C1A2=160°,∠A2C2A3=80°,∠A3C3A4=40°,∠A4C4A5=20°,…
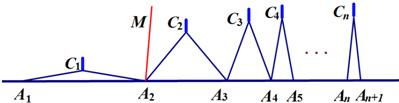
(1)①由题意可得∠A1A2C1=______°;
②若A2M平分∠A3A2C1,则∠MA2C2=______°;
(2)∠An+1AnCn=______°(用含n的代数式表示);
(3)当n≥3时,设∠An-1AnCn-1的度数为a,∠An+1AnCn-1的角平分线AnN与AnCn构成的角的度数为β,那么a与β之间的等量关系是______,请说明理由.(提示:可以借助下面的局部示意图)
查看习题详情和答案>>
小知识:如图,我们称两臂长度相等(即CA=CB)的圆规为等臂圆规。当等臂圆规的两脚摆放在一条直线上时,若张角∠ACB=x°,则底角∠CAB=∠CBA=(90-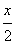 )°请运用上述知识解决问题: 如图,n个相同规格的等臂圆规的两脚依次摆放在同一条直线上,其张角度数变化如下:
)°请运用上述知识解决问题: 如图,n个相同规格的等臂圆规的两脚依次摆放在同一条直线上,其张角度数变化如下:
∠A1C1A2=160°,∠A2C2A3=80°,∠A3C3A4=40°,∠A4C4A5=20°,…
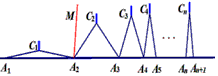
(1)①由题意可得∠A1A2C1=_________;
②若A2M平分∠A3A2C1,则∠MA2C2=__________;
(2)∠An+1AnCn____________;(用含n的代数式表示)
(3)当n≥3时,设∠An-1AnCn-1的度数为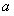 ,∠An+1AnCn-1的角平分线AnM与AnCn构成的角的度数为
,∠An+1AnCn-1的角平分线AnM与AnCn构成的角的度数为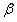 ,那么
,那么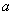 与
与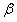 之间的等量关系是__________,请说明理由。(提示:可以借助下面的局部示意图)
之间的等量关系是__________,请说明理由。(提示:可以借助下面的局部示意图)
②若A2M平分∠A3A2C1,则∠MA2C2=__________;
(2)∠An+1AnCn____________;(用含n的代数式表示)
(3)当n≥3时,设∠An-1AnCn-1的度数为
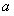 ,∠An+1AnCn-1的角平分线AnM与AnCn构成的角的度数为
,∠An+1AnCn-1的角平分线AnM与AnCn构成的角的度数为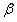 ,那么
,那么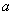 与
与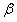 之间的等量关系是__________,请说明理由。(提示:可以借助下面的局部示意图)
之间的等量关系是__________,请说明理由。(提示:可以借助下面的局部示意图)