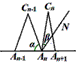题目内容
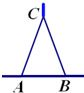 小知识:如图,我们称两臂长度相等(即CA=CB)的圆规为等臂圆规.当等臂圆规的两脚摆放在一条直线上时,若张角∠ACB=x°,则底角∠CAB=∠CBA=(90-
小知识:如图,我们称两臂长度相等(即CA=CB)的圆规为等臂圆规.当等臂圆规的两脚摆放在一条直线上时,若张角∠ACB=x°,则底角∠CAB=∠CBA=(90- )°.
)°.
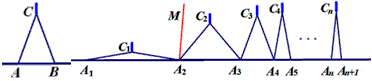
请运用上述知识解决问题:如图,n个相同规格的等臂圆规的两脚依次摆放在同一条直线上,其张角度数变化如下:∠A1C1A2=160°,∠A2C2A3=80°,∠A3C3A4=40°,∠A4C4A5=20°,…
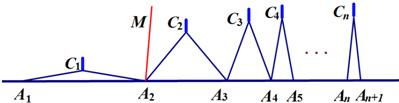
(1)①由题意可得∠A1A2C1=______°;
②若A2M平分∠A3A2C1,则∠MA2C2=______°;
(2)∠An+1AnCn=______°(用含n的代数式表示);
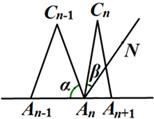
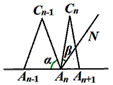
(3)当n≥3时,设∠An-1AnCn-1的度数为a,∠An+1AnCn-1的角平分线AnN与AnCn构成的角的度数为β,那么a与β之间的等量关系是______,请说明理由.(提示:可以借助下面的局部示意图)
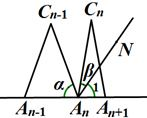 解:(1)①10;②35;
解:(1)①10;②35;(2)∠An+1AnCn是△An+1AnCn的底角,顶角是:
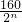 =
= °,则
°,则)∠An+1AnCn=
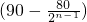 °;(注:写成
°;(注:写成 的不扣分,丢掉括号的不扣分)
的不扣分,丢掉括号的不扣分)(3)α-β=45°;理由:不妨设∠Cn-1=k.
根据题意可知,
 .在△AnAn-1Cn-1中,由小知识可知∠An-1AnCn-1=
.在△AnAn-1Cn-1中,由小知识可知∠An-1AnCn-1= .∴∠An+1AnCn-1=180°-α=
.∴∠An+1AnCn-1=180°-α= .
.在△An+1AnCn中,由小知识可知∠An+1AnCn=
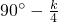 .
.∵AnN平分∠An+1AnCn-1,
∴∠1=
 ∠An+1AnCn-1=
∠An+1AnCn-1= .
.∵∠An+1AnCn=∠1+∠CnAnN,
∴
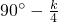 =
=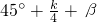 .
.∴
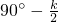 =45°+β.
=45°+β.∴α=45°+β.
∴α-β=45°.
分析:利用角的和差关系计算,注意利用等腰三角形的性质.
点评:本题主要考查等腰三角形的性质:等腰三角形的两个底角相等.

练习册系列答案
相关题目
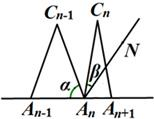
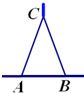 小知识:如图,我们称两臂长度相等(即CA=CB)的圆规为等臂圆规.当等臂圆规的两脚摆放在一条直线上时,若张角∠ACB=x°,则底角∠CAB=∠CBA=(90-
小知识:如图,我们称两臂长度相等(即CA=CB)的圆规为等臂圆规.当等臂圆规的两脚摆放在一条直线上时,若张角∠ACB=x°,则底角∠CAB=∠CBA=(90-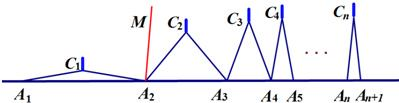
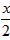 )°,
)°,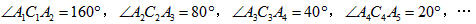
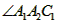 =____°;
=____°;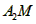 平
平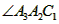 ,则
,则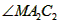 =____°;
=____°;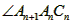 =____°(用含n的代数式表示);
=____°(用含n的代数式表示);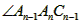 的度数为a,
的度数为a,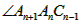 的角平分线
的角平分线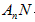 与
与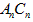 构成的角的度数为β,那么α与β之间的等量关系是____,请说明理由。(提示:可以借助上面的局部示意图)
构成的角的度数为β,那么α与β之间的等量关系是____,请说明理由。(提示:可以借助上面的局部示意图) 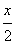 )°请运用上述知识解决问题: 如图,n个相同规格的等臂圆规的两脚依次摆放在同一条直线上,其张角度数变化如下:
)°请运用上述知识解决问题: 如图,n个相同规格的等臂圆规的两脚依次摆放在同一条直线上,其张角度数变化如下: 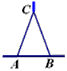
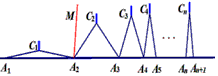
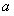 ,∠An+1AnCn-1的角平分线AnM与AnCn构成的角的度数为
,∠An+1AnCn-1的角平分线AnM与AnCn构成的角的度数为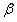 ,那么
,那么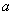 与
与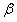 之间的等量关系是__________,请说明理由。(提示:可以借助下面的局部示意图)
之间的等量关系是__________,请说明理由。(提示:可以借助下面的局部示意图)