摘要：又,且,所以 ---
网址：http://m.1010jiajiao.com/timu_id_474077[举报]
有以下四个命题：
①底面是三角形，其余的各面是全等的等腰三角形的棱锥是正三棱锥;②底面是三角形，侧面和底面所在的平面所成的锐二面角相等的棱锥是正三棱锥;③一个棱锥是正棱锥的充分必要条件是底面多边形既有内切圆，又有外接圆，而且是同心圆;④一个四棱锥是正四棱锥的充分但不必要条件是各侧面是等边三角形.
其中真命题的个数是( )
A.0 B.1 C.2 D.3
查看习题详情和答案>>从以下两个小题中选做一题(只能做其中一个，做两个按得分最低的记分)．(甲)一水池有2个进水口，1个出水口，每口进出水速度如图甲、乙所示．某天0点到6点，该水池的蓄水量如图丙所示．(至少打开一个水口)
给出以下3个论断：①0点到3点只进水不出水；②3点到4点不进水只出水；③4点到6点不进水不出水．则一定能确定正确的论断序号是________．
(乙)深圳市的一种特色水果上市时间仅能持续5个月，预测上市初期和后期会因供不应求使价格呈连续上涨态势，而中期又将出现供大于求使价格连续下跌，现有三种价格模拟函数．①f(x)p·qx;②f(x)＝px2＋qx＋1;③f(x)＝x(x－q)2＋p
(以上三式中p，q均为常数，且q＞1，x＝0表示4月1日，x＝1表示5月1日，依次类推)．
(1)为准确研究其价格走势，应选________种价格模拟函数．
(2)若f(x)＝4，f(2)＝6，预测该果品在________月份内价格下跌．
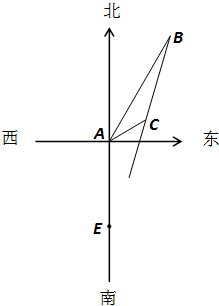如图所示，在一个特定时段内，以点E为中心的10海里以内海域被设为警戒水域．点E正北40| 3 |
| 3 |
（1）求该船的行驶速度（单位：海里/小时）；
（2）若该船不改变航行方向继续行驶．判断它是否会进入警戒水域，并说明理由．
给出以下三个命题，其中所有正确命题的序号为
①已知等差数列{an}的前n项和为Sn，
，
为不共线向量，又
=a1
+a2012
，若
=λ
，则S2012=1006．
②“a=
dx”是函数“y=cos2（ax）-sin2（ax）的最小正周期为4”的充要条件；
③已知函数f（x）=|x2-2|，若f（a）=f（b），且0＜a＜b，则动点P（a，b）到直线4x+3y-15=0的距离的最小值为1．
查看习题详情和答案>>
①
①
①已知等差数列{an}的前n项和为Sn，
| AO |
| OB |
| OP |
| OA |
| OB |
| PA |
| PB |
②“a=
| ∫ | 1 0 |
| 1-x2 |
③已知函数f（x）=|x2-2|，若f（a）=f（b），且0＜a＜b，则动点P（a，b）到直线4x+3y-15=0的距离的最小值为1．
给出以下五个命题，其中所有正确命题的序号为
①函数f(x)=
+2
的最小值为l+2
；
②已知函数f （x）=|x2-2|，若f （a）=f （b），且0＜a＜b，则动点P（a，b）到直线4x+3y-15=0的距离的最小值为1；
③命题“函数f（x）=xsinx+1，当x1，x2∈[-
，
]，且|x1|＞|x2|时，有f （x1）＞f（x2）”是真命题；
④“a=
dx”是函数“y=cos2（ax）-sin2（ax）的最小正周期为4”的充要条件；
⑤已知等差数列{an}的前n项和为Sn，
，
为不共线向量，又
=a
+a2012
，若
=λ
，则S2012=2013．
查看习题详情和答案>>
①③
①③
①函数f(x)=
| x2-2x |
| x2-5x+4 |
| 2 |
②已知函数f （x）=|x2-2|，若f （a）=f （b），且0＜a＜b，则动点P（a，b）到直线4x+3y-15=0的距离的最小值为1；
③命题“函数f（x）=xsinx+1，当x1，x2∈[-
| π |
| 2 |
| π |
| 2 |
④“a=
| ∫ | 1 0 |
| 1-x2 |
⑤已知等差数列{an}的前n项和为Sn，
| OA |
| OB |
| OP |
| OA |
| OB |
| PA |
| PB |