题目内容
有以下四个命题：①底面是三角形，其余的各面是全等的等腰三角形的棱锥是正三棱锥;②底面是三角形，侧面和底面所在的平面所成的锐二面角相等的棱锥是正三棱锥;③一个棱锥是正棱锥的充分必要条件是底面多边形既有内切圆，又有外接圆，而且是同心圆;④一个四棱锥是正四棱锥的充分但不必要条件是各侧面是等边三角形.
其中真命题的个数是( )
A.0 B.1 C.2 D.3
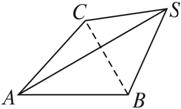
思路解析：如图所示，三棱锥S—ABC中，SA=SC=BA=BC=1，AC=SB=2.
则△SAC≌△ASB≌△CSB.
很明显S—ABC不是正三棱锥，故①是假命题；
如图所示，三棱锥S—ABC中，侧面与底面所成的锐二面角相等，而S在平面ABC上的射影在△ABC的外部，很明显S—ABC不是正三棱锥，故②是假命题；
平面多边形既有内切圆，又有外接圆，而且是同心圆，那么这个多边形是正多边形，但顶点在底面上的射影的位置不明确，故③是假命题；
各侧面是等边三角形的棱锥必是正四棱锥，但正四棱锥的各侧面不一定是等边三角形，故④是真命题.故选B.
答案：B
练习册系列答案
相关题目
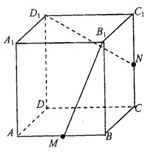16、如图所示，在正方体ABCD-A1B1C1D1中，M、N分别是棱AB、CC1的中点，△MB1P的顶点P在棱CC1与棱C1D1上运动，有以下四个命题：