网址:http://m.1010jiajiao.com/timu_id_4724[举报]
说明:
1、 本解答仅给出了一种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容对照评分标准制定相应的评分细则。
2、 评阅试卷,应坚持每题评阅到底,不要因为考生的解答中出现错误而中断对该题的评阅,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定后续部分的给分,但不得超过该部分正确解答应得分数的一半,如果后续部分的解答有较严重的错误,就不给分。
3、 解答右端所注分数,表示考生正确做到这一步应得的累加分数。
4、 给分或扣分以1分为单位,选择题和填空题不给中间分。
一、选择题:本题考查基本知识和基本运算。每小题5分,满分50分。
1.B 2.C 3.B 4.A 5.A 6.C 7.D 8.B 9.D 10.C
二、填空题:本题考查基本知识和基本运算。每小题5分,满分30分。
11.; 12.; 13.; 14.; 15.; 16.6
三、解答题
17、
-----------------------------------------------3分
令 知 , .
故函数的图象的对称中心的坐标为 () ------------6分
(II)由 得
平方得 -------------------------9分
又 故 ,
∴
即 --------------------------------------12分
18、(Ⅰ)设“甲恰好负两局”的事件为A,“甲恰好胜三局”的事件为B.则
P(A)=, ---------------------------------3分
∵P(A)≤P(B) ∴≤,解得P≥
由0<P<1,得 --------------------------------5分
(Ⅱ)设“四局比赛后未结束比赛”的事件为C
四局比赛后未结束比赛包含甲3:1领先乙,甲2:2平乙,乙3:1领先甲---------7分
∴ -------------------------9分
=
= -----------------------11分
答:四局比赛后未结束比赛的概率为。 -----------------------12分
或:=
∵∠ABC=900 ∴AB⊥BC
故BC⊥平面SAB -----------------3分
(Ⅱ) 延长CD、BA交于点P,连接SP
则SP为平面SCD与平面SAB的交线
----------------------------5分
由条件计算可得∠BSP=900
由(Ⅰ) BC⊥平面SAB
故SC⊥SP
∴∠CSB就是平面SCD与平面SAB
所成的二面角的平面角
-----------------------------7分
在Rt△CSB中sin∠CSB=
∴平面SCD与平面SAB所成的二面角的正弦值为 ---------------------9分
(Ⅲ) 答:在SD上存在点F,使得DF∥平面BED。---------------------10分
连接AC与BD交于点O,连接OE,
在三角形SAC中,过点A作AM∥OE设交SC于点M,---------------------12分
在三角形SDC中过点M作ED的平行线与SD交于F,连接AF
则面AMF∥面EBD
又AF平面EBD,故AF∥平面BED
∴在SD上是存在一点F,使AF∥平面BED ----------------------------14分
20、(Ⅰ) 设椭圆方程为(a>b>0)
由e==得a2=3b2, ---------------------------------------------2分
故椭圆方程为,
,A(0,b)
------------------------------4分
∴
∴椭圆方程为 ------------------------------7分
(Ⅱ)设,显然≠1,由于与同向,故=-----------8分
设,D(m,n),则(x0,y0-2)= (m,n-2)
∴ ------------------------------10分
由C、D在椭圆上得
消去m得, --------------------13分
又∵ ∴ 解得
故的取值范围是 ------------------------16分
21、(Ⅰ) --------------------------------------1分
过切点P1(x1,y1)的切线方程为
由于切线过原点O,因此
解得 -------------------------------------4分
(Ⅱ) 过切点Pn+1(xn+1,yn+1)的切线方程为
由于切线过点Pn(xn,yn),因此-- ---6分
化简得,∴ -------------------------------8分
即,
∴数列是以为首项,公比为的等比数列。 ---------------9分
(Ⅲ)由(Ⅱ)得=
------------------------------------11分
令,由错位相减可求得
-----------------------------13分
∴=,由单调性得 ∴
要使对恒成立, 故
∴的取值范围是。----------------------------------16分
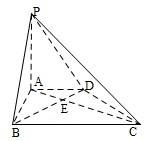 如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=4,AD=2,AB=2
如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=4,AD=2,AB=2| 3 |
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)求二面角A-PC-D的大小. 查看习题详情和答案>>
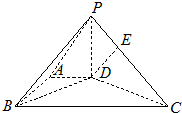 如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PD⊥面ABCD.AD=1,AB=
如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PD⊥面ABCD.AD=1,AB=| 3 |
(1)求证:BD⊥PC;
(2)求直线AB与平面PDC所成角;
(3)设点E在棱PC、上,
| PE |
| PC |
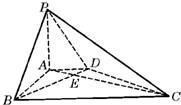 如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=3,AD=2,AB=2
如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=3,AD=2,AB=2| 3 |
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)求二面角P-BD-A的大小. 查看习题详情和答案>>
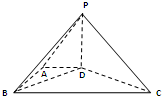 如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PD⊥平面ABCD.AD=1,AB=
如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PD⊥平面ABCD.AD=1,AB=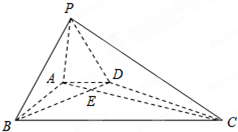 如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD.PA=3,AD=2,AB=2
如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD.PA=3,AD=2,AB=2