题目内容
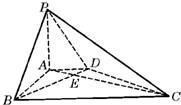 如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=3,AD=2,AB=2
如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=3,AD=2,AB=2| 3 |
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)求二面角P-BD-A的大小.
分析:解法一:(I)由已知中底面为直角梯形的四棱锥P-ABCD中,∠ABC=90°,且PA⊥平面ABCD,我们结合线面垂直的性质及勾股定理,可以得到BD与平面PAC中两个相交直线PA,AC均垂直,进而根据线面垂直的判定定理得到BD⊥平面PAC;
(Ⅱ)连接PE,可得∠AEP为二面角P-BD-A的平面角,解三角形AEP即可得到二面角P-BD-A的大小.
解法二:(I)以A为坐标原点,建立空间坐标系,根据向量垂直,数量积为零,判断出BD⊥AP,BD⊥AC,再由线面垂直的判定定理得到BD⊥平面PAC;
(Ⅱ)分别求出平面PBD与平面ABD的一个法向量,代入向量夹角公式,即可得到二面角P-BD-A的大小.
(Ⅱ)连接PE,可得∠AEP为二面角P-BD-A的平面角,解三角形AEP即可得到二面角P-BD-A的大小.
解法二:(I)以A为坐标原点,建立空间坐标系,根据向量垂直,数量积为零,判断出BD⊥AP,BD⊥AC,再由线面垂直的判定定理得到BD⊥平面PAC;
(Ⅱ)分别求出平面PBD与平面ABD的一个法向量,代入向量夹角公式,即可得到二面角P-BD-A的大小.
解答:解法一:(Ⅰ)∵PA⊥平面ABCD,BD?平面ABCD.∴BD⊥PA.
又tanABD=
=
,tanBAC=
=
.∴∠ABD=30°,∠BAC=60°,∴∠AEB=90°,即BD⊥AC.
又PA∩AC=A.∴BD⊥平面PAC.
…..(6分)
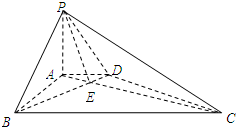
(Ⅱ)连接PE.∵BD⊥平面PAC.∴BD⊥PE,BD⊥AE.∴∠AEP为二面角P-BD-A的平面角.
在Rt△AEB中,AE=AB•sinABD=
,
∴tanAEP=
=
,∴∠AEP=60°,∴二面角P-BD-A的大小为60°. …..(12分)
解法二:(Ⅰ)如图,建立坐标系,
则A(0,0,0),B(2
,0,0),C(2
,6,0),D(0,2,0),P(0,0,3),
∴
=(0,0,3),
=(2
,6,0),
=(-2
,2,0),∴
•
=0,
•
=0.
∴BD⊥AP,BD⊥AC,
又PA∩AC=A,∴BD⊥面PAC.
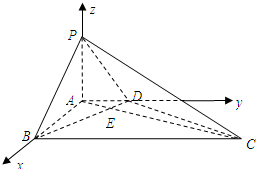
(Ⅱ)设平面ABD的法向量为m=(0,0,1),
设平面PBD的法向量为n=(x,y,1),
则n•
=0,n•
=0∴
解得
∴n=(
,
,1).
∴cos<m,n>=
=
.∴二面角P-BD-A的大小为60°.
又tanABD=
| AD |
| AB |
| ||
| 3 |
| BC |
| AB |
| 3 |
又PA∩AC=A.∴BD⊥平面PAC.
…..(6分)

(Ⅱ)连接PE.∵BD⊥平面PAC.∴BD⊥PE,BD⊥AE.∴∠AEP为二面角P-BD-A的平面角.
在Rt△AEB中,AE=AB•sinABD=
| 3 |
∴tanAEP=
| AP |
| AE |
| 3 |
解法二:(Ⅰ)如图,建立坐标系,
则A(0,0,0),B(2
| 3 |
| 3 |
∴
| AP |
| AC |
| 3 |
| BD |
| 3 |
| BD |
| AP |
| BD |
| AC |
∴BD⊥AP,BD⊥AC,
又PA∩AC=A,∴BD⊥面PAC.

(Ⅱ)设平面ABD的法向量为m=(0,0,1),
设平面PBD的法向量为n=(x,y,1),
则n•
| BP |
| BD |
|
|
| ||
| 2 |
| 3 |
| 2 |
∴cos<m,n>=
| m•n |
| |m||n| |
| 1 |
| 2 |
点评:本题考查的知识点是用空间向量求平面间的夹角,直线与平面垂直的判定,(I)的关键是熟练掌握空间中直线与平面垂直的判定定理,(II)的关键法一是得到∠AEP为二面角P-BD-A的平面角,法二是求出平面PBD与平面ABD的一个法向量.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 如图,已知棱锥P-ABCD的底面ABCD为直角梯 形,AB∥CD,AB⊥BC,CD=PB=BC=1,
如图,已知棱锥P-ABCD的底面ABCD为直角梯 形,AB∥CD,AB⊥BC,CD=PB=BC=1, 如图,在四棱锥P-ABCD中,底面为直角梯ABCD,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别为PC,PB的中点.
如图,在四棱锥P-ABCD中,底面为直角梯ABCD,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别为PC,PB的中点. 如图,在四棱锥P-ABCD中,底面为直角梯ABCD,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别为PC,PB的中点.
如图,在四棱锥P-ABCD中,底面为直角梯ABCD,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别为PC,PB的中点.
