题目内容
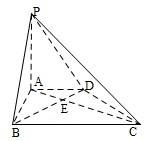如图，在底面为直角梯形的四棱锥P-ABCD中，AD∥BC，∠ABC=90°，PA⊥平面ABCD，PA=4，AD=2，AB=2| 3 |
（Ⅰ）求证：BD⊥平面PAC；
（Ⅱ）求二面角A-PC-D的大小．
分析：（Ⅰ）要证BD⊥平面PAC，只需证明BD垂直平面PAC内的两条相交直线PA，AC即可．
（Ⅱ）过E作EF⊥PC，垂足为F，连接DF，说明∠EFD为二面角A-PC-D的平面角，推出Rt△EFC∽Rt△PAC，通过解Rt△EFD，求二面角A-PC-D的大小．
（Ⅱ）过E作EF⊥PC，垂足为F，连接DF，说明∠EFD为二面角A-PC-D的平面角，推出Rt△EFC∽Rt△PAC，通过解Rt△EFD，求二面角A-PC-D的大小．
解答：
证明：（Ⅰ）∵PA⊥平面ABCD，BD?平面ABCD．∴BD⊥PA．
又tanABD=
=
，tanBAC=
=
．∴∠ABD=30°，∠BAC=60°，∴∠AEB=90°，即BD⊥AC．
又PA∩AC=A．∴BD⊥平面PAC
（Ⅱ）过E作EF⊥PC，垂足为F，连接DF．
∵DE⊥平面PAC，EF是DF在平面PAC上的射影，由三垂线定理知PC⊥DF，∴∠EFD为二面角A-PC-D的平面角．
又∠DAC=90°-∠BAC=30°，
∴DE=ADsinDAC=1，AE=ABsinABE=
，
又AC=4
，∴EC=3
，PC=8．
由Rt△EFC∽Rt△PAC得EF=
=
．
在Rt△EFD中，tanEFD=
=
，∴∠EFD=arctan
．
∴二面角A-PC-D的大小为arctan
．
证明：（Ⅰ）∵PA⊥平面ABCD，BD?平面ABCD．∴BD⊥PA．又tanABD=
| AD |
| AB |
| ||
| 3 |
| BC |
| AB |
| 3 |
又PA∩AC=A．∴BD⊥平面PAC
（Ⅱ）过E作EF⊥PC，垂足为F，连接DF．
∵DE⊥平面PAC，EF是DF在平面PAC上的射影，由三垂线定理知PC⊥DF，∴∠EFD为二面角A-PC-D的平面角．
又∠DAC=90°-∠BAC=30°，
∴DE=ADsinDAC=1，AE=ABsinABE=
| 3 |
又AC=4
| 3 |
| 3 |
由Rt△EFC∽Rt△PAC得EF=
| PA•EC |
| PC |
3
| ||
| 2 |
在Rt△EFD中，tanEFD=
| DE |
| EF |
2
| ||
| 9 |
2
| ||
| 9 |
∴二面角A-PC-D的大小为arctan
2
| ||
| 9 |
点评：本题考查平面与平面垂直的判定，二面角及其度量，考查逻辑思维能力，空间想象能力，计算能力，是中档题．
练习册系列答案
考前必练系列答案
相关题目
如图，已知棱锥P-ABCD的底面ABCD为直角梯 形，AB∥CD，AB⊥BC，CD=PB=BC=1，
如图，在四棱锥P-ABCD中，底面为直角梯ABCD，AD∥BC，∠BAD=90°，PA⊥底面ABCD，且PA=AD=AB=2BC，M，N分别为PC，PB的中点．
如图，在四棱锥P-ABCD中，底面为直角梯ABCD，AD∥BC，∠BAD=90°，PA⊥底面ABCD，且PA=AD=AB=2BC，M，N分别为PC，PB的中点．
