题目内容
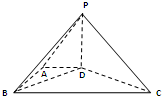 如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PD⊥平面ABCD.AD=1,AB=
如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PD⊥平面ABCD.AD=1,AB=| 3 |
(1)求证:BD⊥PC;
(2)求直线AB与平面PDC所成角的大小.
分析:(1)在△BDC中,可得出BD2+DC2=BC2,即BD⊥DC,再由PD⊥平面ABCD,BD⊥平面ABCD从而BD⊥PC,
(2)由(1)可得DH∥AB,DH与平面PDC所成角的平面角即为AB与平面PDC所成角,过G作GH垂直DC于G,面PCD⊥平面ABCD,,HG⊥平面PCD∠HGD为直线AB与平面PDC所成角的平面角.在直角三角形△DHC中求解即可.
(2)由(1)可得DH∥AB,DH与平面PDC所成角的平面角即为AB与平面PDC所成角,过G作GH垂直DC于G,面PCD⊥平面ABCD,,HG⊥平面PCD∠HGD为直线AB与平面PDC所成角的平面角.在直角三角形△DHC中求解即可.
解答:解:(1)如图.作DH⊥BC于H,在直角△DHC中,DH=AB=
,HC=3,∴DC=2
,又在直角△BAD中,BD=2,在△BDC中,BD2+DC2=BC2,∴BD⊥DC,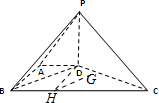
∵PD⊥平面ABCD,PD?平面PCD
∴平面PCD⊥平面ABCD,
∴BD⊥平面PCD,PC?平面PCD
∴BD⊥PC;
(2)由(1)可得DH∥AB∴DH与平面PDC所成角的平面角即为AB与平面PDC所成角
过G作GH垂直DC于G,
∵平面PCD⊥平面ABCD,∴HG⊥平面PCD
∠HGD为直线AB与平面PDC所成角的平面角.
在直角三角形△DHC中,sin∠HGD=
=
=
,∠HGD=
直线AB与平面PDC所成角的大小为
.
| 3 |
| 3 |

∵PD⊥平面ABCD,PD?平面PCD
∴平面PCD⊥平面ABCD,
∴BD⊥平面PCD,PC?平面PCD
∴BD⊥PC;
(2)由(1)可得DH∥AB∴DH与平面PDC所成角的平面角即为AB与平面PDC所成角
过G作GH垂直DC于G,
∵平面PCD⊥平面ABCD,∴HG⊥平面PCD
∠HGD为直线AB与平面PDC所成角的平面角.
在直角三角形△DHC中,sin∠HGD=
| HC |
| DC |
| 3 | ||
2
|
| ||
| 2 |
| π |
| 3 |
直线AB与平面PDC所成角的大小为
| π |
| 3 |
点评:本题考查线线、线面位置关系、线面角的求解.考查空间想象能力、计算能力.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 如图,已知棱锥P-ABCD的底面ABCD为直角梯 形,AB∥CD,AB⊥BC,CD=PB=BC=1,
如图,已知棱锥P-ABCD的底面ABCD为直角梯 形,AB∥CD,AB⊥BC,CD=PB=BC=1, 如图,在四棱锥P-ABCD中,底面为直角梯ABCD,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别为PC,PB的中点.
如图,在四棱锥P-ABCD中,底面为直角梯ABCD,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别为PC,PB的中点. 如图,在四棱锥P-ABCD中,底面为直角梯ABCD,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别为PC,PB的中点.
如图,在四棱锥P-ABCD中,底面为直角梯ABCD,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别为PC,PB的中点.
