摘要:得则所求椭圆方程为.
网址:http://m.1010jiajiao.com/timu_id_471380[举报]
如图,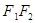 分别是椭圆
分别是椭圆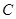 :
: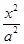 +
+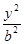 =1(
=1(
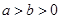 )的左、右焦点,
)的左、右焦点,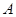 是椭圆
是椭圆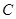 的顶点,
的顶点,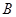 是直线
是直线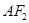 与椭圆
与椭圆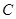 的另一个交点,
的另一个交点,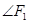
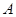
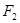 =60°.
=60°.
(Ⅰ)求椭圆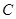 的离心率;
的离心率;
(Ⅱ)已知△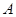
 的面积为40
的面积为40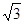 ,求
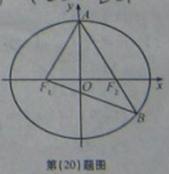
,求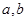 的值.
的值.
【解析】 (Ⅰ)由题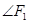
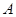
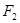 =60°,则
=60°,则 ,即椭圆
,即椭圆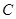 的离心率为
的离心率为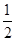 。
。
(Ⅱ)因△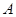
 的面积为40
的面积为40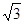 ,设
,设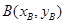 ,又面积公式
,又面积公式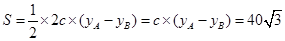 ,又直线
,又直线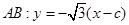 ,
,
又由(Ⅰ)知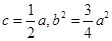 ,联立方程可得
,联立方程可得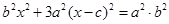 ,整理得
,整理得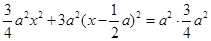 ,解得
,解得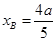 ,
,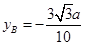 ,所以
,所以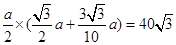 ,解得
,解得 。
。
查看习题详情和答案>>
已知以坐标原点为中心的椭圆,满足条件
(1)焦点F1的坐标为(3,0);
(2)长半轴长为5.
则可求得此椭圆方程为![]() =1(※)
=1(※)
问可用其他什么条件代替条件(2),使所求得的椭圆方程仍为(※)?请写出两种替代条件,并说明理由.
查看习题详情和答案>>已知以坐标原点为中心的椭圆,满足条件:
(1)焦点F1的坐标为(3,0);
(2)长半轴长为5.
则可求得此椭圆方程为![]() =1(※),问可用其他什么条件代替条件(2),使所求得的椭圆方程仍为(※)?请写出两种替代条件,并说明理由.
=1(※),问可用其他什么条件代替条件(2),使所求得的椭圆方程仍为(※)?请写出两种替代条件,并说明理由.
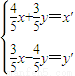 可把平面直角坐标系上的一点P(x,y)变换到这一平面上的一点P′(x′,y′).
可把平面直角坐标系上的一点P(x,y)变换到这一平面上的一点P′(x′,y′).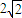 ,长轴顶点和短轴顶点间的距离为2.求该椭圆C的标准方程,并求出其两个焦点F1、F2经变换公式T变换后得到的点F1′和F2′的坐标;
,长轴顶点和短轴顶点间的距离为2.求该椭圆C的标准方程,并求出其两个焦点F1、F2经变换公式T变换后得到的点F1′和F2′的坐标;