题目内容
现有变换公式T: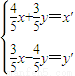 可把平面直角坐标系上的一点P(x,y)变换到这一平面上的一点P′(x′,y′).
可把平面直角坐标系上的一点P(x,y)变换到这一平面上的一点P′(x′,y′).(1)若椭圆C的中心为坐标原点,焦点在x轴上,且焦距为
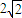 ,长轴顶点和短轴顶点间的距离为2.求该椭圆C的标准方程,并求出其两个焦点F1、F2经变换公式T变换后得到的点F1′和F2′的坐标;
,长轴顶点和短轴顶点间的距离为2.求该椭圆C的标准方程,并求出其两个焦点F1、F2经变换公式T变换后得到的点F1′和F2′的坐标;(2)若曲线M上一点P经变换公式T变换后得到的点P'与点P重合,则称点P是曲线M在变换T下的不动点.求(1)中的椭圆C在变换T下的所有不动点的坐标;
(3)在(2)的基础上,试探究:中心为坐标原点、对称轴为坐标轴的椭圆和双曲线在变换T下的不动点的存在情况和个数.
【答案】分析:(1)先根据题a2-b2=2,a2+b2=4,联立方程组,求的a和b,则椭圆方程方程可得.根据椭圆的性质可气的焦点坐标,代入变换公式中即可求的点F1′和F2′的坐标.
(2)依题意设不动点P的坐标为(m,n)依题意则有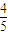 m+
m+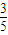 n=m,求的m和n的关系代入椭圆方程中求的n和m,则不动点坐标可得.
n=m,求的m和n的关系代入椭圆方程中求的n和m,则不动点坐标可得.
(3)设曲线M在变换T下的不动点P(x,y)分情况看椭圆和双曲线时,先根据变换公式求的x和y的关系,代入椭圆或双曲线方程看方程得解.
解答:解:(1)依题意可知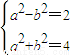 解得a2=3,b2=1
解得a2=3,b2=1
∴椭圆方程为 ,焦点坐标为F1(
,焦点坐标为F1(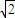 ,0),F2(-
,0),F2(-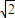 ,0)
,0)
依题意F1′的坐标为(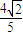 ,
,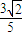 ),F2′(-
),F2′(-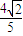 ,-
,-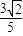 )
)
(2)依题意设不动点P的坐标为(m,n)依题意则有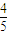 m+
m+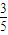 n=m,整理的m=3n,代入椭圆方程得
n=m,整理的m=3n,代入椭圆方程得
 ,解得n=
,解得n= ,m=
,m= 或n=-
或n=- ,m=-
,m=-
∴不动点坐标为( ,
, )(-
)(- ,-
,- )
)
(3)由(2)可知,曲线M在变换T下的不动点P(x,y)需满足
情形一:据题意,不妨设椭圆方程为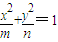 (m>0,n>0),
(m>0,n>0),
则有 .
.
因为m>0,n>0,所以 恒成立,
恒成立,
因此椭圆在变换T下的不动点必定存在,且一定有2个不动点.
情形二:设双曲线方程为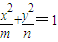 (mn<0),
(mn<0),
则有 ,因为mn<0,
,因为mn<0,
故当9n+m=0时,方程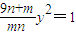 无解;
无解;
当9n+m≠0时,故要使不动点存在,则需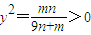 ,
,
因此,当且仅当 时,双曲线在变换T下一定有2个不动点.否则不存在不动点.
时,双曲线在变换T下一定有2个不动点.否则不存在不动点.
进一步分类可知,
(i)当n<0,m>0时,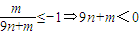
 .
.
即双曲线的焦点在
轴上时,需满足 时,双曲线在变换
时,双曲线在变换
下一定有2个不动点.否则不存在不动点.
(ii)当n>0,m<0时,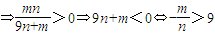 .
.
即双曲线的焦点在y轴上时,需满足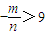 时,双曲线在变换T下一定有2个不动点.否则不存在不动点.
时,双曲线在变换T下一定有2个不动点.否则不存在不动点.
点评:本题主要考查了圆锥曲线的共同特征.考查了学生对圆锥曲线知识的综合掌握.
(2)依题意设不动点P的坐标为(m,n)依题意则有
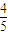 m+
m+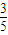 n=m,求的m和n的关系代入椭圆方程中求的n和m,则不动点坐标可得.
n=m,求的m和n的关系代入椭圆方程中求的n和m,则不动点坐标可得.(3)设曲线M在变换T下的不动点P(x,y)分情况看椭圆和双曲线时,先根据变换公式求的x和y的关系,代入椭圆或双曲线方程看方程得解.
解答:解:(1)依题意可知
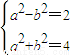 解得a2=3,b2=1
解得a2=3,b2=1∴椭圆方程为
 ,焦点坐标为F1(
,焦点坐标为F1(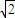 ,0),F2(-
,0),F2(-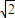 ,0)
,0)依题意F1′的坐标为(
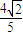 ,
,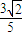 ),F2′(-
),F2′(-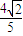 ,-
,-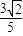 )
)(2)依题意设不动点P的坐标为(m,n)依题意则有
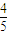 m+
m+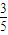 n=m,整理的m=3n,代入椭圆方程得
n=m,整理的m=3n,代入椭圆方程得 ,解得n=
,解得n= ,m=
,m= 或n=-
或n=- ,m=-
,m=-
∴不动点坐标为(
 ,
, )(-
)(- ,-
,- )
)(3)由(2)可知,曲线M在变换T下的不动点P(x,y)需满足
情形一:据题意,不妨设椭圆方程为
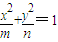 (m>0,n>0),
(m>0,n>0),则有
 .
.因为m>0,n>0,所以
 恒成立,
恒成立,因此椭圆在变换T下的不动点必定存在,且一定有2个不动点.
情形二:设双曲线方程为
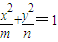 (mn<0),
(mn<0),则有
 ,因为mn<0,
,因为mn<0,故当9n+m=0时,方程
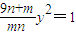 无解;
无解;当9n+m≠0时,故要使不动点存在,则需
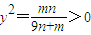 ,
,因此,当且仅当
 时,双曲线在变换T下一定有2个不动点.否则不存在不动点.
时,双曲线在变换T下一定有2个不动点.否则不存在不动点.进一步分类可知,
(i)当n<0,m>0时,
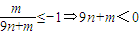
 .
.即双曲线的焦点在
轴上时,需满足
 时,双曲线在变换
时,双曲线在变换下一定有2个不动点.否则不存在不动点.
(ii)当n>0,m<0时,
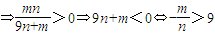 .
.即双曲线的焦点在y轴上时,需满足
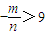 时,双曲线在变换T下一定有2个不动点.否则不存在不动点.
时,双曲线在变换T下一定有2个不动点.否则不存在不动点.点评:本题主要考查了圆锥曲线的共同特征.考查了学生对圆锥曲线知识的综合掌握.

练习册系列答案
相关题目