摘要:20 先化简再求值. (1) x-2(x-y2)+(-x+y2),其中x=-1,y=. (2).已知x+y=7,xy=2,求 ①2x2+2y2的值, ②(x-y)2的值.
网址:http://m.1010jiajiao.com/timu_id_450146[举报]
选择与填空每题3分
1.D
2.D 点拨:图中的邻补角分别是:∠AOC与∠BOC,∠AOC与∠AOD,∠COE与∠DOE,∠BOE与∠AOE,∠BOD与∠BOC,∠AOD与∠BOD,共6对,故选D.
3.B 4.B 5.D 6.D
7.B
8.A
9.C
10.A
11.B点拨:∠FCD=∠F=∠A=∠1=∠ABG=45°.
故选D.
12.D
13.略 14.略 15.略
16.-4ab
17.红球
18.145º
19.略 每题4分
(2)90 (3分) 41(3分)
21(7分)答图,由邻补角的定义知∠BOC=100°.
∵OD,OE分别是∠AOB,∠BOC的平分线,
∴∠DOB= ∠AOB=40°,∠BOE=
∠AOB=40°,∠BOE= ∠BOC=50°.
∠BOC=50°.
∴∠DOE=∠DOB+∠BOE=40°+50°=90°.
22.(7分)解:CD⊥AB,FE⊥AB,∴CD∥EF,
∴∠2=∠FCD.
∵∠1=∠2,∴∠1=∠FCD.
∴DG∥BC.∴∠BCA=∠3=80°.
23.(7分) 列方程解得边长为
24.(7分)有两个角,有一种不平行。作出一种给3分。
25.(6分)解:AB∥CD.
理由:如答图,过点F作FH∥AB,则∠AEF+∠EFH=180°.
∵∠AEF=150°,∴∠EFH=30°.
又∵EF⊥GF,∴∠HFG=90°-30°=60°.
又∵∠DGF=60°,
∴∠HFG=∠DGF.
∴HF∥CD,从而可得AB∥CD.

(1)计算:-22+(tan60°-1)×
+(-
)-2+(-π)0-|2-
|;
(2)先化简再求值(1+
)÷
,其中x=3.
(3)物理兴趣小组20位同学在实验操作中的得分情况如下表: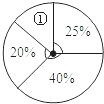
问:①求这20位同学实验操作得分的众数,中位数;
②这20位同学实验操作得分的平均分是多少?
③将此次操作得分按人数制成如图所示的扇形统计图.扇形①的圆心角度数是多少? 查看习题详情和答案>>
| 3 |
| 1 |
| 2 |
| 3 |
(2)先化简再求值(1+
| 1 |
| x-2 |
| x2-1 |
| 2x-4 |
(3)物理兴趣小组20位同学在实验操作中的得分情况如下表:

| 得分(分) | 10 | 9 | 8 | 7 |
| 人数(人) | 5 | 8 | 4 | 3 |
②这20位同学实验操作得分的平均分是多少?
③将此次操作得分按人数制成如图所示的扇形统计图.扇形①的圆心角度数是多少? 查看习题详情和答案>>
(1)计算:-22+(tan60°-1)×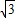 +(-
+(- )-2+(-π)-|2-
)-2+(-π)-|2- |;
|;
(2)先化简再求值 ,其中x=3.
,其中x=3.
(3)物理兴趣小组20位同学在实验操作中的得分情况如下表:
问:①求这20位同学实验操作得分的众数,中位数;
②这20位同学实验操作得分的平均分是多少?
③将此次操作得分按人数制成如图所示的扇形统计图.扇形①的圆心角度数是多少?
 查看习题详情和答案>>
查看习题详情和答案>>
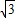 +(-
+(- )-2+(-π)-|2-
)-2+(-π)-|2- |;
|;(2)先化简再求值
 ,其中x=3.
,其中x=3.(3)物理兴趣小组20位同学在实验操作中的得分情况如下表:
| 得分(分) | 10 | 9 | 8 | 7 |
| 人数(人) | 5 | 8 | 4 | 3 |
②这20位同学实验操作得分的平均分是多少?
③将此次操作得分按人数制成如图所示的扇形统计图.扇形①的圆心角度数是多少?
 查看习题详情和答案>>
查看习题详情和答案>>
(1)计算:-22+(tan60°-1)× +(-
+(- )-2+(-π)-|2-
)-2+(-π)-|2-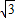 |;
|;
(2)先化简再求值 ,其中x=3.
,其中x=3.
(3)物理兴趣小组20位同学在实验操作中的得分情况如下表:
问:①求这20位同学实验操作得分的众数,中位数;
②这20位同学实验操作得分的平均分是多少?
③将此次操作得分按人数制成如图所示的扇形统计图.扇形①的圆心角度数是多少?
 查看习题详情和答案>>
查看习题详情和答案>>
 +(-
+(- )-2+(-π)-|2-
)-2+(-π)-|2-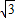 |;
|;(2)先化简再求值
 ,其中x=3.
,其中x=3.(3)物理兴趣小组20位同学在实验操作中的得分情况如下表:
| 得分(分) | 10 | 9 | 8 | 7 |
| 人数(人) | 5 | 8 | 4 | 3 |
②这20位同学实验操作得分的平均分是多少?
③将此次操作得分按人数制成如图所示的扇形统计图.扇形①的圆心角度数是多少?
 查看习题详情和答案>>
查看习题详情和答案>>
