摘要：15．解:(1)∵∠ACB=90°.∴AC⊥BC．又∵DE⊥BC.∴EF∥AC．又∵AE∥CF.∴四边形EACF是平行四边形．当CF=AC时.四边形ACFE是菱形．
网址：http://m.1010jiajiao.com/timu_id_446729[举报]
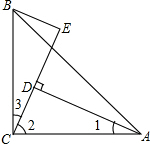
阅读并填空：如图，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于点E，AD⊥CE于点D．请说明△ADC≌△CEB的理由．
解：∵BE⊥CE于点E（已知），
∴∠E=90°
（垂直的意义）
（垂直的意义）
，同理∠ADC=90°，
∴∠E=∠ADC（等量代换）．
在△ADC中，
∵∠1+∠2+∠ADC=180°
（三角形的内角和等于180°）
（三角形的内角和等于180°）
，∴∠1+∠2=90°
（等式的性质）
（等式的性质）
．∵∠ACB=90°（已知），
∴∠3+∠2=90°，
∴
∠1=∠3（同角的余角相等）
∠1=∠3（同角的余角相等）
．在△ADC和△CEB中，.
|
∴△ADC≌△CEB （A．A．S）
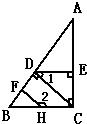
22、如图，已知AC⊥BC，CD⊥AB，DE⊥AC，∠1与∠2互补，判断HF与AB是否垂直，并说明理由（填空）．解：垂直．理由如下：
∵DE⊥AC，AC⊥BC，
∴∠AED=∠ACB=90°（垂直的意义）
∴DE∥BC（
同位角相等，两直线平行
）∴∠1=∠DCB（
两直线平行，内错角相等
）∵∠1与∠2互补（已知），
∴∠DCB与∠2互补
∴
FH
∥CD
（同旁内角互补，两直线平行
）∴
∠BFH
=∠CDB（两直线平行，同位角相等
）∵CD⊥AB，∴∠CDB=90°，∴∠HFB=90°，∴HF⊥AB．
如图，在△ABC中，已知∠ACB=90°，CD⊥AB于D，AC=6
，BD=3．
（1）请根据下面求cosA的解答过程，在横线上填上适当的结论，使解答正确完整，
∵CD⊥AB，∠ACB=90°∴AC= cosA， =AC•cosA
由已知AC=6
，BD=3，∴6
=AB cosA=（AD+BD）cosA=（6
cosA+3）cosA，设t=cosA，则t＞0，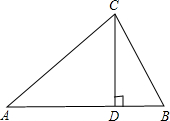
且上式可化为2
t2+ =0，则此解得cosA=t=
；
（2）求BC的长及△ABC的面积． 查看习题详情和答案>>
| 3 |
（1）请根据下面求cosA的解答过程，在横线上填上适当的结论，使解答正确完整，
∵CD⊥AB，∠ACB=90°∴AC=
由已知AC=6
| 3 |
| 3 |
| 3 |
且上式可化为2| 3 |
| ||
| 2 |
（2）求BC的长及△ABC的面积． 查看习题详情和答案>>
如图，DG⊥BC，AC⊥BC，EF⊥AB，∠1=∠2，说明CD⊥AB的理由．