题目内容
 如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,说明CD⊥AB的理由.
如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,说明CD⊥AB的理由.解:因为DG⊥BC,AC⊥BC
已知
已知
所以∠DGB=90°∠ACB=90°(垂直的意义)
所以∠DGB=∠ACB
等量代换
等量代换
所以DG∥AC
同位角相等,两直线平行
同位角相等,两直线平行
所以∠2=
∠3
∠3
因为∠1=∠2
已知
已知
所以∠1=
∠3
∠3
所以EF∥CD
同位角相等,两直线平行
同位角相等,两直线平行
所以∠AEF=∠
ADC
ADC
因为EF⊥AB
已知
已知
所以∠AEF=90°
垂直定义
垂直定义
所以∠ADC=90°
等量代换
等量代换
所以CD⊥AB
垂直定义
垂直定义
.分析:根据解题过程和平行线的性质与判定填空.
解答:解:∵DG⊥BC,AC⊥BC,(已知),
∴∠DGB=90°∠ACB=90°,
∴∠DGB=∠ACB=90°(等量代换),
∴DG∥AC(同位角相等,两直线平行),
∴∠2=∠3,(两直线平行,内错角相等).
∵∠1=∠2(已知),
∴∠1=∠3.
∴EF∥CD,(同位角相等,两直线平行).
∴∠AEF=∠ADC(两直线平行,同位角相等).
∵EF⊥AB(已知),
∴∠AEF=90°(垂直定义).
∴∠ADC=90°,
即CD⊥AB(垂直定义).
∴∠DGB=90°∠ACB=90°,
∴∠DGB=∠ACB=90°(等量代换),
∴DG∥AC(同位角相等,两直线平行),
∴∠2=∠3,(两直线平行,内错角相等).
∵∠1=∠2(已知),
∴∠1=∠3.
∴EF∥CD,(同位角相等,两直线平行).
∴∠AEF=∠ADC(两直线平行,同位角相等).
∵EF⊥AB(已知),
∴∠AEF=90°(垂直定义).
∴∠ADC=90°,
即CD⊥AB(垂直定义).
点评:本题主要考查解题的依据,需要熟练掌握平行线的性质与判定.应用平行线的判定和性质定理时,一定要弄清题设和结论,切莫混淆.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
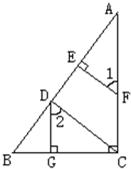 25、已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.
25、已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB. 26、在括号内填写理由.(1)如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE.
26、在括号内填写理由.(1)如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE. 证明:∵DG⊥BC,AC⊥BC(
证明:∵DG⊥BC,AC⊥BC(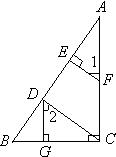 25、请为下面题目的说明过程加上理由.
25、请为下面题目的说明过程加上理由. 已知,如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2.请问CD与AB有什么位置关系?并且说明理由.
已知,如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2.请问CD与AB有什么位置关系?并且说明理由.