��Ŀ����
����˵�����ٵ�m��1ʱ����ʽ
�������壻��������������y=
��ͼ���㣨
��
��������ÿ����֧��y����x����������۹���x�ķ���
-2=
�������⣬��m��6������Rt��ABC�У���ACB=90�㣬BC=a��AC=b��AB=c��AB���ϵĸ�CD=h����ô��
��
��
��Ϊ�ߵ���������ֱ�������Σ�������ȷ�Ľ��۵ĸ����ǣ�������
| 1 |
| x2-2x+m |
| k |
| x |
| -m |
| 3 | 3m |
| x |
| x-3 |
| m |
| x-3 |
| 1 |
| a |
| 1 |
| b |
| 1 |
| h |
�������ٽ�x2-2x+m�䷽���ٸ���m��1�жϷ�ĸ�ķ��ţ�
�ڱ�����������Ϊm��0����k=xy�ж�k�ķ��ţ�
������⣬�ٸ���x��0��x��3��m��ȡֵ��Χ��
�����ù��ɶ������涨�������жϣ�
�ڱ�����������Ϊm��0����k=xy�ж�k�ķ��ţ�
������⣬�ٸ���x��0��x��3��m��ȡֵ��Χ��
�����ù��ɶ������涨�������жϣ�
����⣺�١�x2-2x+m=��x-1��2+m-1���൱m��1ʱ��x2-2x+m��0����ʽ�����壬������ȷ��
����
�������֪��m��0����k=
•
��0��ͼ���ڶ��������ޣ���ÿ����֧��y����x���������������ȷ��
�۽ⷽ�̵�x=6-m����x��0�ɵ�m��6����x��3����m��3����ӦΪm��6��m��3�����۴���
�������⣬��a2+b2=c2��ab=ch�����ԣ�
+
=
=
=
��������ȷ��
��ȷ����������
��ѡC��
����
| -m |
| -m |
| 3 | 3m |
�۽ⷽ�̵�x=6-m����x��0�ɵ�m��6����x��3����m��3����ӦΪm��6��m��3�����۴���
�������⣬��a2+b2=c2��ab=ch�����ԣ�
| 1 |
| a2 |
| 1 |
| b2 |
| a2+b2 |
| a2b2 |
| c2 |
| c2h2 |
| 1 |
| h2 |
��ȷ����������
��ѡC��
���������⿼���˹��ɶ��������涨������ʽ���̵Ľ⣬����������ͼ���ϵ�������ص㣮�ؼ����������ո�֪ʶ��Ľ��ⷽ����

��ϰ��ϵ�д�
 ��ѧ�̸̳����¿α�ϵ�д�
��ѧ�̸̳����¿α�ϵ�д� Сѧ��ʱ��ѵϵ�д�
Сѧ��ʱ��ѵϵ�д�
�����Ŀ
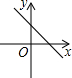 ��֪����y=kx+b��ͼ����ͼ��ʾ������ں���y=
��֪����y=kx+b��ͼ����ͼ��ʾ������ں���y=| kb |
| x |
| A����x����ʱ��yҲ���� |
| B����x����ʱ��y��С |
| C���ú�����ͼ��λ��һ�������� |
| D���ú�����ͼ��λ�ڶ��������� |
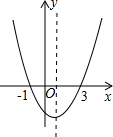 ���κ���y=ax2+bx+c��ͼ����ͼ��ʾ����������˵���У�
���κ���y=ax2+bx+c��ͼ����ͼ��ʾ����������˵���У�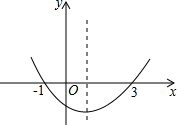 ���κ���y=ax2+bx+c��ͼ����ͼ����������˵����
���κ���y=ax2+bx+c��ͼ����ͼ����������˵����