摘要:已知函数y=f(x)是定义在区间[-.]上的偶函数.且x∈[0.]时.f(x)=-x2-x+5的解析式, (2)若矩形ABCD的顶点A.B在函数y=f(x)的图象上.顶点C.D在x轴上.求矩形ABCD面积的最大值. 解 (1)当x∈[-.0]时.-x∈[0.]. ∴f2-(-x)+5=-x2+x+5. 又∵f=f(-x)=-x2+x+5. ∴f(x)= (2)由题意.不妨设A点在第一象限.坐标为(t,-t2-t+5),其中t∈(0.]. 由图象对称性可知B点坐标为(-t.-t2-t+5).则S(t)=S矩形ABCD=2t(-t2-t+5)=-2t3-2t2+10t. =-6t2-4t+10.由=0.得t1=-.t2=1.当0<t<1时.>0;t>1时,<0. ∴S(t)在(0.1]上单调递增.在[1.]上单调递减.∴当t=1时.矩形ABCD的面积取得极大值6. 且此极大值也是S(t)在t∈(0.]上的最大值.从而当t=1时.矩形ABCD的面积取得最大值6.
网址:http://m.1010jiajiao.com/timu_id_4463577[举报]
(2008•南京模拟)某电视台的一个智力游戏节目中,有一道将四本由不同作者所著的外国名著A、B、C、D与它们的作者连线的题目,每本名著只能与一名作者连线,每名作者也只能与一本名著连线.每连对一个得3分,连错得-1分,一名观众随意连线,他的得分记作ξ.
(1)求该观众得分ξ为非负的概率;
(2)求ξ的分布列及数学期望.
查看习题详情和答案>>
(1)求该观众得分ξ为非负的概率;
(2)求ξ的分布列及数学期望.
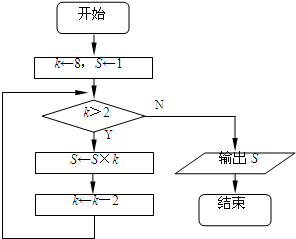 (2008•南京模拟)如图所示的流程图输出的结果是
(2008•南京模拟)如图所示的流程图输出的结果是