题目内容
(2008•南京模拟)某电视台的一个智力游戏节目中,有一道将四本由不同作者所著的外国名著A、B、C、D与它们的作者连线的题目,每本名著只能与一名作者连线,每名作者也只能与一本名著连线.每连对一个得3分,连错得-1分,一名观众随意连线,他的得分记作ξ.
(1)求该观众得分ξ为非负的概率;
(2)求ξ的分布列及数学期望.
(1)求该观众得分ξ为非负的概率;
(2)求ξ的分布列及数学期望.
分析:(1)根据题意可得:其连对题目的个数为:0,1,2,4,所以ξ的可能取值为-4,0,4,12,再分别计算出其得分为非负的概率,进而得到答案.
(2)由题意可得:P(ξ=-4)=
=
,再结合(1)可得ξ的分布列与其数学期望.
(2)由题意可得:P(ξ=-4)=
| 9 | ||
|
| 9 |
| 24 |
解答:解:(1)因为直接计算ξ的数值比较困难,
所以首先计算其连对题目的个数.
根据题意可得:其连对题目的个数为:0,1,2,4,
所以ξ的可能取值为-4,0,4,12. …(1分)
因为名观众随意连线,所以有A44种不同的连法,
所以P(ξ=12)=
=
;…(3分)
P(ξ=4)=
=
=
;…(5分)
P(ξ=0)=
=
=
;…(7分)
所以该同学得分非负的概率为P(ξ=12)+P(ξ=4)+P(ξ=0)=
=
.…(8分)
(2)由题意可得:P(ξ=-4)=
=
=
.
所以ξ的分布列为:
…(10分)
所以数学期望Eξ=-4×
+4×
+12×
=0.…(12分)
所以首先计算其连对题目的个数.
根据题意可得:其连对题目的个数为:0,1,2,4,
所以ξ的可能取值为-4,0,4,12. …(1分)
因为名观众随意连线,所以有A44种不同的连法,
所以P(ξ=12)=
| 1 | ||
|
| 1 |
| 24 |
P(ξ=4)=
| ||
|
| 6 |
| 24 |
| 1 |
| 4 |
P(ξ=0)=
| ||
|
| 8 |
| 24 |
| 1 |
| 3 |
所以该同学得分非负的概率为P(ξ=12)+P(ξ=4)+P(ξ=0)=
| 15 |
| 24 |
| 5 |
| 8 |
(2)由题意可得:P(ξ=-4)=
| 9 | ||
|
| 9 |
| 24 |
| 3 |
| 8 |
所以ξ的分布列为:
| ξ | -4 | 0 | 4 | 12 | ||||||||
| P |
|
|
|
|
所以数学期望Eξ=-4×
| 3 |
| 8 |
| 1 |
| 4 |
| 1 |
| 24 |
点评:解决此类问题的关键是熟练掌握排列、组合与计数原理的有关知识,以及等可能事件的概率公式与离散型随机变量的分布列、数学期望等知识,此题属于中档题,是高考命题的热点之一.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
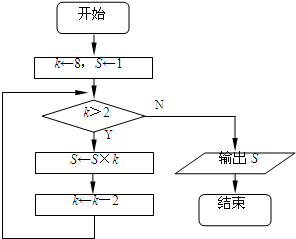 (2008•南京模拟)如图所示的流程图输出的结果是
(2008•南京模拟)如图所示的流程图输出的结果是