摘要:如图所示的是某池塘中的浮萍蔓延的面积y(m 2)与时间t(月)的关系:y=at,有以下叙述:①这个指数函数的底数为2,②第5 个月时.浮萍面积就会超过30 m2;③浮萍从4 m2蔓延到12 m2需要经过1.5个月,④浮萍每月增加的面积都相等,⑤若浮萍蔓延到2 m2.3 m2.6 m2所经过的时间分别为t1.t2.t3,则t1+t2=t3.其中正确的是 ( ) ?A.①② ?B.①②③④ ?C.②③④⑤ ?D.①②⑤ 答案?D? 例1计算:(1) (2)2 (3) 解 (1)方法一 利用对数定义求值 设 则 ∴x=-1. 方法二 利用对数的运算性质求解 (2)原式= = (3)原式= = = = 例2比较下列各组数的大小. (1)log3与log5, (2)log1.10.7与log1.20.7, (3)已知比较2b,2a,2c的大小关系. 解 (1)∵log3<log31=0, 而log5>log51=0,∴log3<log5. (2)方法一 ∵0<0.7<1,1.1<1.2, ∴0>log0.71.1>log0.71.2, ∴ 即由换底公式可得log1.10.7<log1.20.7. 方法二 作出y=log1.1x与y=log1.2x的图象. 如图所示两图象与x=0.7相交可知log1.10.7<log1.20.7. (3)∵y=为减函数.且 ∴b>a>c,而y=2x是增函数.∴2b>2a>2c. 例3=logax .如果对于任意x∈[3.+∞)都有|f(x)|≥1成立.试求a的取值范围. 解 当a>1时.对于任意x∈[3.+∞).都有f(x)>0. 所以.|f=logax在[3.+∞)上为增函数. ∴对于任意x∈[3.+∞).有f(x)≥loga3. 4分 因此.要使|f(x)|≥1对于任意x∈[3.+∞)都成立. 只要loga3≥1=logaa即可.∴1<a≤3. 6分 当0<a<1时.对于x∈[3.+∞).有f(x)<0, ∴|f. 8分 ∵f(x)=logax在[3.+∞)上为减函数. ∴-f上为增函数. ∴对于任意x∈[3.+∞)都有|f≥-loga3. 10分 因此.要使|f(x)|≥1对于任意x∈[3.+∞)都成立. 只要-loga3≥1成立即可. ∴loga3≤-1=loga,即≤3,∴≤a<1. 综上.使|f(x)|≥1对任意x∈[3.+∞)都成立的a的取值范围是:(1.3]∪[.1). 12分 例4 已知过原点O的一条直线与函数y=log8x的图象交于A.B两点.分别过A.B作y轴的平行线与函数y=log2x的图象交于C.D两点. (1)证明:点C.D和原点O在同一直线上, (2)当BC平行于x轴时.求点A的坐标. (1)证明 设点A.B的横坐标分别为x1.x2, 由题设知x1>1,x2>1, 则点A.B的纵坐标分别为log8x1.log8x2. 因为A.B在过点O的直线上. 所以 点C.D的坐标分别为(x1,log2x1).(x2,log2x2), 由于log2x1==3log8x1,log2x2=3log8x2, OC的斜率为k1= OD的斜率为k2= 由此可知k1=k2,即O.C.D在同一直线上. (2)解 由于BC平行于x轴.知log2x1=log8x2. 即得log2x1=log2x2,x2=, 代入x2log8x1=x1log8x2.得 由于x1>1,知log8x1≠0,故=3x1, 又因x1>1,解得x1=, 于是点A的坐标为(.log8).
网址:http://m.1010jiajiao.com/timu_id_4463479[举报]
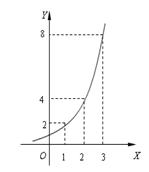
 如图所示的是某池塘中的浮萍蔓延的面积(m2)与时间(月)的关系:y=ax(a>0且a≠1),有以下叙述:
如图所示的是某池塘中的浮萍蔓延的面积(m2)与时间(月)的关系:y=ax(a>0且a≠1),有以下叙述:①这个指数函数的底数是2;
②第5个月时,浮萍的面积就会超过30m2;
③若浮萍蔓延到2m2、3m2、6m2所经过的时间分别为t1、t2、t3,则t1+t2=t3,其中正确的序号是
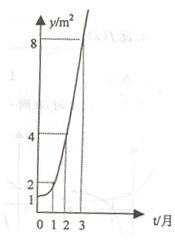
 10、如图所示的是某池塘中的浮萍蔓延的面积(m2)与时间t(月)的关系:y=at,有以下叙述:
10、如图所示的是某池塘中的浮萍蔓延的面积(m2)与时间t(月)的关系:y=at,有以下叙述:①这个指数函数的底数是2;②第5个月时,浮萍的面积就会超过30m2;③浮萍从4m2蔓延到12m2需要经过1.5个月;④浮萍每个月增加的面积都相等;其中正确的是( )
查看习题详情和答案>>
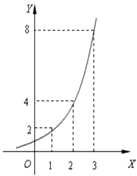 如图所示的是某池塘中的浮萍蔓延的面积(m2)与时间x(月)的关系:y=ax,有以下叙述:
如图所示的是某池塘中的浮萍蔓延的面积(m2)与时间x(月)的关系:y=ax,有以下叙述:①这个指数函数的底数是2;
②第5个月的浮萍的面积就会超过30m2;
③浮萍从4m2蔓延到12m2需要经过1.5个月;
④浮萍每个月增加的面积都相等;
⑤若浮萍蔓延到2m2、3m2、6m2所经过的时间分别为x1,x2,x3,则x1+x2=x3.
其中正确的是( )
| A、①② | B、①②⑤ | C、①②③④ | D、②③④⑤ |
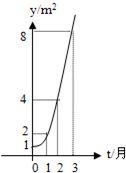 20、如图所示的是某池塘中的浮萍蔓延的面积y(m2)与时间t(月)的关系:y=at,请解决以下问题:
20、如图所示的是某池塘中的浮萍蔓延的面积y(m2)与时间t(月)的关系:y=at,请解决以下问题: 与时间
与时间 (月)的关系:
(月)的关系: ,有以下叙述:① 这个指数函数的底数是2;②第5个月的浮萍的面积就会超过
,有以下叙述:① 这个指数函数的底数是2;②第5个月的浮萍的面积就会超过 ;③浮萍从
;③浮萍从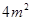 蔓延到
蔓延到 需要经过1.5个月;④浮萍每个月增加的面积都相等;⑤若浮萍蔓延到
需要经过1.5个月;④浮萍每个月增加的面积都相等;⑤若浮萍蔓延到 、
、 、
、 所经过的时间分别为
所经过的时间分别为 ,则
,则 .其中正确的是( )
.其中正确的是( )